Пусть одна диагональ равна 2х, другая - 2у, тогда 2х+2у=24 и х+у-12, откуда у=12-х.
Диагонали ромба пересекаются под прямым углом, таким образом, площадь ромба состоит из 4-х прямоугольны треугольников с катетами х и у, т.е. площадь ромба S=4*0.5xy=2xy.
Подставим сюда у=12-х и получим S=24x-2x^2.
Найдём максимум этой функции. S'= 24-4x.
Стационарная точка: 24-4х=0 х=6
При х=7 S'<0; при х=5 S'>0, следовательно при х=5 имеем максимум S.
у=12-х=12-6=6.
Тогда Smax=2*6*6=72.
Интересно, что получился квадрат с диагоналями, равными 12.
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(−∞,∞)
Нотация построения множества:
{x|x∈R}
Область значений - это набор всех допустимых значений y.Используйте график для определения области значений.
Запись в виде интервала:
(−∞,1]
Определяем область определения и область значений.
Область определения:
(−∞,∞),{x|∈R}
Область значений:
(−∞,1],{y|y≤1}
Объяснение:
4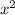 -12х+9+9
-12х+9+9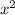 -16+42х=13
-16+42х=13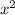 +30х-7
+30х-7
при х=-2
13*4-60-7=-15
Объяснение: