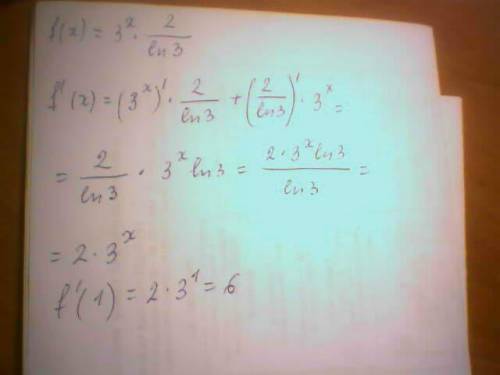
х- скорость велосипедиста на пути из А в В
х+9 - скорость велосипедиста на пути из В в А
162/х=162/(х+9)+9
162/х=(162+9х+81)/(х+9)
162х+1458=162х+9х^2+81x
-9x^2-81x+1458=0
x^2+9x-162=0
решаем квадратное уравнение
а=1
b=9
c=-162
D=b^2-4ac=9^2-4*1*-162=81+648=729
1 корень= (-b+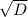
)/2a=(-9+27)*2=18/2=9
2 корень= (-b-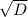)/2a=(-9-27)*2=-36/2=-18
скорость не может быть отрицательной, поэтому пожходит только 1 корень
х=9 (км/ч)- скорость велосипедиста на пути из А в В
9+9=18 (км/ч)- скорость велосипедиста на пути из В в А
1) Х - расстояние, которое проехали мотоцикл и автомобиль от поста ДПС,
Х/60 - время движения мотоцикла от поста ДПС,
Х/90 - время движения автомобиля от поста ДПС,
мотоцикл ехал от поста ДПС на 1 час больше , чем автомобиль,
Х/60 = Х/90 + 1
90 Х = 60 Х + 5400
30 Х = 5400
Х = 180. Автомобиль догнал мотоцикл на расстоянии 180 км от поста ДПС
2) Пусть скорость В=х
тогда скорость А=х+1
время в пути В = 10:х
время в пути А = 9:(х+1) +0,5
10:х=9:(х+1) +0,5
10/х -9/(х+1)=0,5
Умножь обе части уравнения на х(х+1)
получится 10(х+1) -9х = 0,5х² +0,5х
10х +10 - 9х = 0,5х² +0,5х
0,5х² -10х+9х +0,5х=0
0,5х² -0,5х -10=0
Решение:
Исходное уравнение имеет вид:
0.5x2-0.5x-10=0
Дискриминант равен:
D=b2-4ac=-0.52-4·0.5·-10=20.25
Так как дискриминант больше нуля, то уравнение имеет два корня
x1= -b+√D/2a = -(-0.5)+√20.25/2·(0.5) = 5;
x2= -b-√D/2a =-(-0.5)-√20.25/2·(0.5)= -4;
Отрицательный корень отбрасываем.
Скорость пешехода из В=5 км/час
Скорость пешехода из А =6 км/час
f'(1)=2*3^1=6