Пара чисел (2;-2) являются точкой пересечения двух графиков. заданных уравнениями системы.
Общее уравнение прямой: Ах+Ву+С=0
х=2; у=-2
1 уравнение: пусть А=4; В=-4, тогда 4х-4у+С=0
4*2-4*(-2)=16
С=0-16=-16
4х-4у-16=0
2 уравнение: пусть А=8; В=1, тогда: 8х+у+С=0
8*2+1*(-2)=14
С=0-14=14
8х+у-14=0
{4x-4y-16=0 => x-y-4=0 => x=y+4
{8x+y-14=0 => 8(y+4)+y-14=0
9y=-18
y=-2
x=-2+4
x=2
Решением данной системы является пара чисел (2;-2)
Проверка: 4x-4y-16=8x+y-14
4х-8х-4у-у-16+14=0
-4х-5у-2=0
х=2; у=-2 - -4*2-5*(-2)-2=
-8+10-2=
-10+10=0
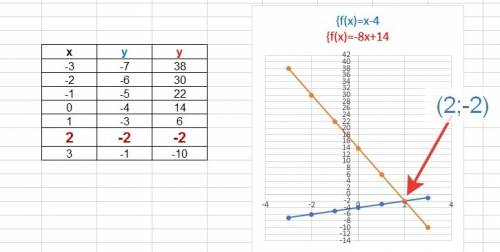
Выразим у через х для графического решения:
{4x-4y-16=0 =>у=х-4
{8x+y-14=0 => у=-8х+14
График во вложении
Исходная матрица имеет вид:
1 2 0
2 4 0
0 0 0
Объяснение:
Составляем систему для определения координат собственных векторов:
(1 - λ)x1 + 2x2 + 0x3 = 0
2x1 + (4 - λ)x2 + 0x3 = 0
0x1 + 0x2 + (0 - λ)x3 = 0
Составляем характеристическое уравнение и решаем его.
1 - λ 2 0
2 4 - λ 0
0 0 0 - λ
Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.
(1 - λ) • ((4 - λ) • (0 - λ)-0 • 0)-2 • (2 • (0 - λ)-0 • 0)+0 • (2 • 0-(4 - λ) • 0) = 0
После преобразований, получаем:
5*λ2-λ3 = 0
λ1 = 0
Подставляя λ1 = 0 в систему, имеем:
1 - 0 2 0
2 4 - 0 0
0 0 0 - 0
или
1 2 0
2 4 0
0 0 0