Объяснение:
думаю что можно составить 2 трёхзначные цифры , это - 246; 310;
246 : 2 = 123
310 : 2 = 155
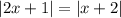
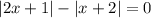
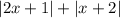
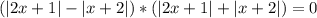
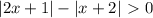
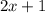 и
и 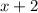 принимают значение
принимают значение 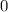 при различных значениях
при различных значениях  , по этому сумма указанных выше двух модулей всегда строго положительна)
, по этому сумма указанных выше двух модулей всегда строго положительна)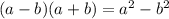 :
: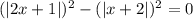
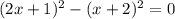
![[(2x+1)-(x+2)]*[(2x+1)+(x+2)]=0](/tpl/images/0599/8070/031a8.png)
![[x-1]*[3x+3]=0](/tpl/images/0599/8070/f7400.png)
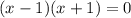
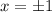
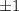


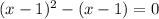

![(x-1)*[(x-1)-(1)]=0](/tpl/images/0599/8070/f134d.png)
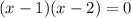
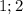
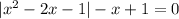
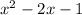
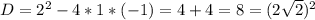
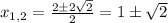
![|[x-(1- \sqrt{2} )]*[x-(1+ \sqrt{2} )]|-x+1=0](/tpl/images/0599/8070/ef287.png)
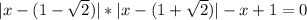
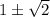 разбивают множество действительных чисел на три интервала:
разбивают множество действительных чисел на три интервала:![x\in(-\infty;1- \sqrt{2}]](/tpl/images/0599/8070/b7e08.png) , то имеем уравнение (оба модуля раскрываются с минусом):
, то имеем уравнение (оба модуля раскрываются с минусом):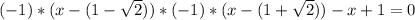
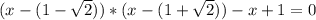
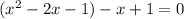
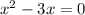
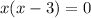
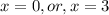
![(-\infty;1- \sqrt{2}]](/tpl/images/0599/8070/ee814.png) , значит из этой ветки корней для исходного уравнения не оказалось
, значит из этой ветки корней для исходного уравнения не оказалось![x\in(1- \sqrt{2};1+ \sqrt{2} ]](/tpl/images/0599/8070/340ea.png) (один модуль раскрывается с минусом, а второй с плюсом), то:
(один модуль раскрывается с минусом, а второй с плюсом), то: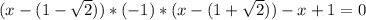
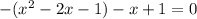
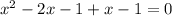
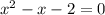
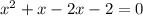
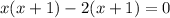
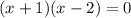
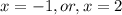
![(1- \sqrt{2};1+ \sqrt{2} ]](/tpl/images/0599/8070/a7e75.png) попадает лишь корень
попадает лишь корень 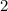 - первое найденное решение исходного уравнения
- первое найденное решение исходного уравнения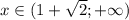 то оба модуля раскрываются с плюсом, и мы получаем точно такое же уравнение, как и в случае 1)
то оба модуля раскрываются с плюсом, и мы получаем точно такое же уравнение, как и в случае 1)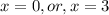 . В указанный интервал попадает лишь корень
. В указанный интервал попадает лишь корень 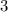 - второе и последнее решение исходного уравнения.
- второе и последнее решение исходного уравнения.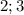
ответ на фото ............
Объяснение:
.......