Сумму всех членов геометрической прогрессии можно найти в том случае, когда она является бесконечно убывающей, т.е. когда lql < 1.
1) √(5/2) = √2,5,
√2,5 > √1, q > 1, прогрессия бесконечно убывающей не является
2) √(3/2) = √1,5,
√1,5 > √1, q > 1, прогрессия бесконечно убывающей не является.
ни в одной из прогрессий сумму всех членов найти нельзя.
Если q = √5/2, то
√5/2 = √(5/4), √1,25 > √1, q > 1, прогрессия бесконечно убывающей не является.
Если q = √3/2, то
√3/2 = √(3/4), √0,75 < √1, q < 1, прогрессия является бесконечно убывающей. Сумму всех её членов найти можно по формуле:
S = b1 / (1 - q).
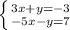
Перечёркиваем +y и -y,остальное слаживаем,получим уравнение:
-2x = 4
x= 4 : (-2)
x = -2
Если x = -2, то
3*(-2) + y = -3
-6 + y = -3
y = 3
ответ: ( -2;3)
2)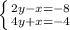
Перечёркиваем +x и -x, слаживаем остальное и получаем уравнение:
6y = -12
y = -12 : 6
y= -2
Если y= -2, то
2 *(-2) - x = -8
-4 - x = -8
-x = -4
x = 4
ответ: (4;-2)
3)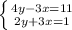
Перечёркиваем -3x и +3x, слаживаем остальное и получаем уравнение:
6y = 12
y = 2
Если y= 2, то
2 * 2 + 3x = 1
4 + 3x = 1
3x = -3
x = -1
ответ:(-1;2)
4)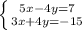
Перечёркиваем -4y и +4y, слаживаем остальное и получаем уравнение:
8x = -8
x = -1
Если x = -1, то
5 * (-1) - 4y = 7
-5 - 4y = 7
-4y = 12
y = -3
ответ: (-1;-3)