8; 18.
Объяснение:
Для решения данной задачи мы будем составлять систему из двух уравнений с двумя неизвестными.
Пусть Х и У - числа.
Сумма этих чисел - по условию - равна 26, то есть Х + У = 26.
Это первое уравнение системы.
Разность чисел - по условию - равна 10, то есть Х - У = 10.
Это второе уравнение системы.
Сведём вместе эти два уравнения в систему:
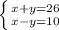
Решим данную систему сложения.
Имеем:
2*х = 36
х = 36 / 2
х = 18
Подставим найденное значение переменной Х в одно из уравнений, например, в первое уравнение составленной нами системы - для определения значения второй переменной:
х + у = 26
18 + у = 26
у = 26 - 18
у = 8
Мы нашли оба значения неизвестных - это числа 18 и 8.
Большее из них - 18. Меньшее - 8.
х³ + у³ = (х+у)(х²+ху+у²) = 10(х²+ху+у²)
чтобы сумма кубов была наименьшей, нужно найти минимум для выражения в скобках (т.к. 10 уже не изменится)))
х²+ху+у² = х²+2ху+у² - ху = (х+у)² - ху = 100 - ху = 100 - (10-у)у =
= 100 - 10у + у² это квадратный трехчлен (график -- парабола, ветви вверх))), своего минимума достигает в вершине параболы...
абсцисса вершины: у₀ = -b / (2a) = 10/2 = 5
тогда х = 10-у = 5
другой вариант рассуждений:
х = 10-у
х³ + у³ = (10-у)³ + у³ = 10³ - 300у + 30у² - у³ + у³ = 30у² - 300у + 1000
вновь парабола, ветви вверх, минимум в вершине для
у₀ = -b / (2a) = 300/(2*30) = 10/2 = 5
тогда х = 5 тоже))