1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
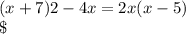
Переобразуем:
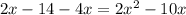
Переносим в общую сторону (левую) и меняем знаки:
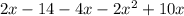
Сокрашаем:
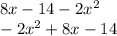
ответ: 
Старший коэффициент: 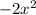
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А) 
В) 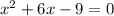
С) 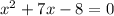
D) 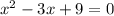
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
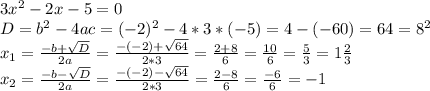
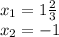
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
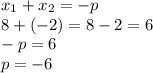


ответ: 
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят  и
и 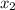 совпадают.
совпадают.
Если p = 0, то 

ответ: c = 32
3. б) Найдите эти корни уравнения
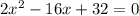
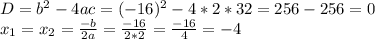
ответ: 
2.Если в четырехугольнике противоположные стороны попарно равны, то это параллелограмм.
3.Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам,то это параллелограмм.
Доказательство первого признака.
Доказательство:Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.Эти треугольники равны между собой по двум сторонам и углу между ними (BD - общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.