
Я в тебя верю, станешь пилотом!
А вот я для тебя решил
А) Тянем первый билет, с вероятностью 3/15 = 1/5 мы вытянем выигрышный билет. Значит, осталось 14 билетов, среди которых уже 2 выигрышных билета. Тянем второй раз, вероятность вытянуть выигрышный билет равна 2/14 = 1/7. Следовательно, вероятность два раза подряд вытащить выигрыш равна 1/5 * 1/7 = 1/35.
б) Здесь надо рассмотреть два случая.
В первый раз вытаскиваем выигрыш (вероятность 3/15=1/5), во второй раз - нет (вероятность 12/14=6/7). Вероятность такой ситуации 1/5 * 6/7 = 6/35.
И другой случай, сперва вытаскиваем билет без выигрыша (вероятность 12/15=4/5), а во второй раз с выигрышем (вероятность 3/14). Вероятность этой ситуации 4/5 * 3/14 = 12/70 = 6/35
Суммируем вероятности обоих случаев 6/35 + 6/35 = 12/35
в) В первый раз не вытянули билет с выигрышем (вероятность 12/15=4/5) и во второй раз (вероятность 11/14). Итоговая вероятность такого варианта развития событий - 4/5 * 11/14 = 22/35
Биквадратное уравнение.
Решается заменой переменной:
Если D >0, т.е.
уравнение имеет корни:
Обратный переход:
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Аналогично
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Если , т.е
, т.е 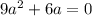
При
уравнение принимает вид:
уравнение не имеет корней
При
уравнение принимает вид:
Уравнение 4-ой степени, значит
О т в е т. При