Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
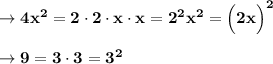
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: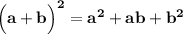 
.
Зная, что первоначально выражение имело вид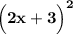 
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
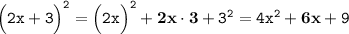
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
