Точка М будет являться серединой отрезка BC, поэтому ее координаты будут
x=(6+2)/2=4
y=(2-6)/2=-2
Теперь найдём длину вектора АМ. Для этого воспользуемся правилом: чтобы найти координаты вектора, нужно из координат конца вычесть координаты начала, т.е.
AM(4-(-2); -2-8)
AM(6;-10)
Теперь найдём длину:
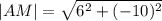
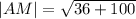
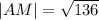
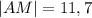
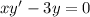 (*)
(*)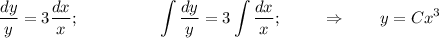
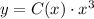 . Тогда, дифференцируя по правилу произведения.
. Тогда, дифференцируя по правилу произведения.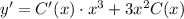
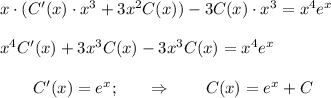
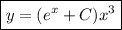

Точка М имеет координаты являющиеся средними координатами точек В(6;2) и С(2;-6)
M((6+2):2;(2+(-6)):2)=(4;-2)
вектор AM=4-(-2);-2-8
его модуль |AM|=sqrt(6^2+(-10)^2)=sqrt(36+100)=sqrt(136) равен длине медианы
ответ:11.6