Question

Решить: исследовать ряды на сходимость. для степенного ряда найти область сходимости: ∞ 1)∑ = 1/ n*5^n n-1 2)∞ ∑ =)^n)*n / 2^n* (n+1) n-1 ∞ 3)∑ = ((n²-5)/5^n)*(x-5)^n n-3

Answer 1

Необходимым условием сходимости ряда, но не достаточным, является стремление общего члена к нулю.

1) $\sum_{n=1}^{\infty}\frac{1}{n5^n}$

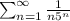
Как видим общий член при n -> ∞ стремится к нулю. Ряд у нас положительный, применим признак Даламбера (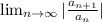$\lim_{n \to \infty} |\frac{a_{n+1}}{a_n}|$)

$\lim_{n \to \infty} \frac{n5^n}{(n+1)5^{n+1}} = \frac{1}{5}<1$

т.е. ряд сходится абсолютно

2) Ряд является знакочередующимся, применим признак Лейбница (Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.)

$\lim_{n \to \infty} |\frac{n}{2^n(n+1)}|=0$

- ряд сходится. Исследуем также на абсолютную и условную сходимости (Сходящийся ∑a(n) называется сходящимся абсолютно, если сходится ряд из модулей ∑|a(n)|, иначе — сходящимся условно.)

$\sum_{n=1}^{\infty}|a_n|=\sum_{n=1}^{\infty}\frac{n}{2^n(n+1)}$

воспользуемся признаком сравнения

$\sum_{n=1}^{\infty}\frac{n}{2^n(n+1)}<\sum_{n=1}^{\infty}\frac{1}{2^n}$

ряд справа сходится, т.е. наш ряд сходится абсолютно.

3) $\sum_{n=3}^{\infty}\frac{n^2-5}{5^n}*(x-5)^n$

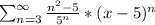
Воспользуемся признаком Даламбера

$\lim_{n \to \infty} \frac{(n+1)^2 - 5}{5^{n+1}}\frac{5^n}{n^2-5}|x-5|=\frac{1}{5}|x-5|$

Наш ряд будет сходится, если ⅕|x-5|<1 ⇔ |x-5|<5 ⇔ -5<x-5<5 ⇔ 0<x<10

Остается исследовать сходимость на концах интервала:

a) x=0

   $\sum_{n=1}^{\infty}\frac{(-5)^n(n^2-5)}{5^n}=\sum_{n=1}^{\infty}(-1)^n(n^2-5)$

ряд расходится

б) x=10

  $\sum_{n=3}^{\infty}\frac{5^n(n^2-5)}{5^n}=\sum_{n=3}^{\infty}(n^2-5)$

ряд расходится

Т.е. область сходимости ряда (0, 10)