ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
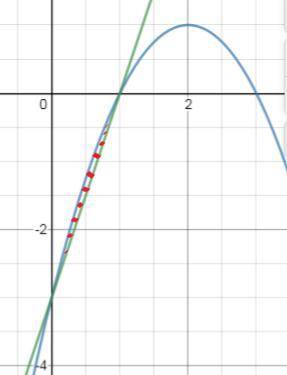
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле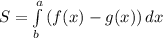 
где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
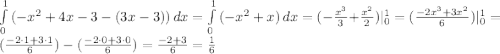
Искомая площадь - S = 1/6 (кв. ед)
решением системы уравнений является набор чисел (здесь 5 и -1), при подстановке которых в эту систему каждое уравнение системы превращается в тождество.
подставляем в х = 5, в у = -1.
1)
5²-(-1)² = 24 ⇒ 25-1=24 ⇒ 24=24
2*25+1 = 22 ⇒ 51≠22
не является решением
2)
25+1 = 26 ⇒26=26
25-1 = -21 ⇒ 24≠-21
не является решением
3)
(5-5)*(-1+2) = 0 ⇒ 0=0
25-2*5*(-1) = 35 ⇒ 25+10 = 35 ⇒ 35=35
пара чисел (5,-1) является решением для этой системы уравнения
4) так же самостоятельно проверь является ли пара чисел (5, -1) решением для 4 системы уравнения. (сразу скажу, там ответ будет отрицательный)
(an=a1+(n-1)d)
a2+a13=a1+d+a1+12d=2a1+13d=77
a6+a15=a1+5d+a1+14d=2a1+19d=107
2a1+13d=77
2a1+19d=107
2a1+19d-(2a1+13d)=107-77
6d=30, d=30/6, d=5
2a1+13d=77, 2a1=77-13d, 2a1=77-13.5=77-65=12,a1=6
a1=6, d=5
(a2=6+5=11, a13=6+60=66, a2+a13=11+66=77
a6=6+25=31, a15=6+70=76, a6+a15=31+76=107)