x - производительность первой бригады
у - производительность 2й бригады
10/х - 10/у = 1
х + у = 4,5
у = 4,5 - х
10у - 10х = ху
45-10х - 10х = х (4,5-х)
х^2 - 4,5x -20x +45=0
x^2 - 24,5 + 45 = 0
D = 24,5^2-180=420,25
x1 = (24,5-20,5)/2 = 2 км
x2 = 45/2 - ( > 4,5 - не годится)
у = 4,5 - х = 2.5 км
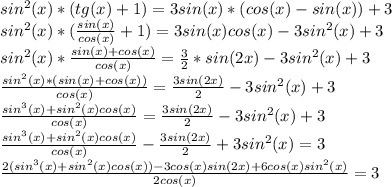
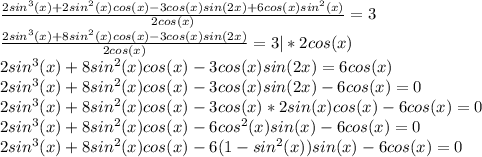
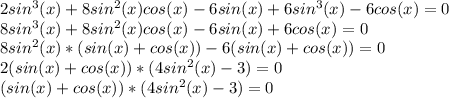
sin(x)+cos(x) = 0 или 4sin²(x)-3 = 0
sin(x) = -cos(x) |:cos(x) 4sin²(x) = 3
tg(x) = -1 sin²(x) = 3/4
x₁ = 3π/4 + πn, n∈Z sin(x) = ±√3/2
sin(x) = -√3/2 или sin(x) = √3/2
x₂ = arcsin(-√3/2) + 2πn x₄ = arcsin(√3/2) + 2πn
x₃ = π-arcsin(-√3/2) + 2πn x₅ = π-arcsin(√3/2) + 2πn
x₂ = -π/3 + 2πn x₄ = π/3 + 2πn
x₃ = π+π/3 + 2πn x₅ = π-π/3 + 2πn
x₂ = 5π/3 + 2πn, n∈Z x₄ = π/3 + 2πn, n∈Z
x₃ = 4π/3 + 2πn, n∈Z x₅ = 2π/3 + 2πn, n∈Z
Следовательно:
x₄ = π/3 + 2πn, n∈Z,
x₅ = 2π/3 + 2πn, n∈Z
ответ: x₁ = 3π/4 + πn, n∈Z;
x₄ = π/3 + 2πn, n∈Z;
x₅ = 2π/3 + 2πn, n∈Z
У драконов по 3 головы, значит число (26 - (головы сороконожек) ) должно быть кратным 3.
Максимум сороконожек могло быть: 298 \ 40 = 7 (штук) , смотрим:
26 - 7 = 19 (не кратно 3)
26 - 6 = 20 (не кратно 3)
26 - 5 = 21 (кратно 3)
26 - 4 = 22 (не кратно 3)
26 - 3 = 23 (не кратно 3)
26 - 2 = 24 (кратно 3)
26 - 1 = 25 (не кратно 3)
26 - 0 = 26 (не кратно 3)
Итак, если сороконожек было 5, то драконов было:
(26 - 5) / 3 = 7
Тогда ног у драконов:
(298 - 5 * 40) / 7 = 14
А если сороконожек было 2, то драконов было:
(26 - 2) / 3 = 8
Тогда ног у драконов:
(298 - 2 * 40) / 8 = 12,25 - этого быть не может.
ответ: У дракона 14 ног.
Пусть х и у ремонтирует каждая бригада. x+y=4,5
вместе они отремонтировали 20 км. t- времяработы
x*t+y(t-1)=20
xt=y(t-1)
решая систему получим квадратное уравнение
2x^2-49x+90=0
x1=2 x2=45/2 - решенение не подходит по ограничкению
x=2 y=2,5
t=5