Question

Решить : найдите общее решение и частное, удовлетворяющее начальным условиям решение дифференциального уравнения первого порядка: 1) y^,=y^3*x, у = 1 при х = 1; 2) *y)/x=x^3*e^x, y0=e, x0=1

Answer 1

1) y' = y³x

 $\frac{dy}{dx} = \frac{y^3}{x}$

Проинтегрируем обе части:

 $\frac{dy}{y^3}=xdx$

$-\frac{1}{2y^2}=\frac{x^2}{2}+C$ - общее решение дифф. уравнения.

Из начального условия y(1)=1 найдем частное решение:

Подставив в общее решение, найдем С

-1/2 = 1/2 + С ⇔ С = -1/4

$y = \frac{4}{1-2x^2}$ - частное решение дифф. уравнения.

2) $y' - \frac{3y}{x}=x^3e^x$

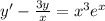
Для начала найдем общее решение однородного дифф. уравнения

$y' - \frac{3y}{x}=0$

$\frac{dy}{dx} = \frac{3y}{x}$

$\frac{dy}{y}=\frac{3dx}{x}$

Проинтегрировав, получим:

ln|y|=3ln|x| + lnC

y = Cx³ - общее решение однородного дифф. уравнения

y = C(x)x³ подставим в наше дифф. уравнение

$C'(x)x^3 + 3x^2C(x) - 3C(x)x^2 = x^3e^x$

$C'(x)=e^x$

$C(x) = \int{e^x}\, dx = e^x + C_1$

$y = (e^x + C_1)x^3$ - общее решение дифф. уравнения

Из начального условия y(1) = e найдем C₁

C₁ = 0

$y = e^xx^3$ - частное решение дифф. уравнения