. Любое число можно представить в виде произведения простых множителей. Запишем:
, где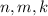 
- некоторые натуральные числа.
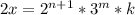является полным квадратом, значит 
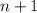и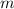 
- четные числа, а 
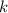- полный квадрат. Аналогично, число 
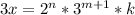является полным кубом, значит 
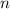и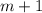 
делятся на 3, а 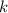- полный куб. 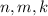это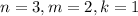 
, значит 
.
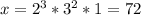y = - x³ + 3x² + 4
Найдём производную :
y' = (- x³)' + 3(x²)' + 4' = - 3x² + 6x
Приравняем производную к нулю , найдём критические точки :
- 3x² + 6x = 0
- 3x(x - 2) = 0
x₁ = 0
x - 2 = 0 ⇒ x₂ = 2
Обе критические точки принадлежат заданному отрезку. Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 3) = -(- 3)³ + 3 * (- 3)² + 4 = 27 + 27 + 4 = 58
y( 3) = - 3³ + 3 * 3² + 4 = - 27 + 27 + 4 = 4
y( 0) = - 0³ + 3 * 0² + 4 = 4
y(2) = - 2³ + 3 * 2² + 4 = - 8 + 12 + 4 = 8
Наименьшее значение функции равно 4, а наибольшее равно 58 .
-4
Объяснение:1. действие: (4х – 7)2 + (5х – 7)(5х + 7) + 140х=16x²-56x+49+25x²-49+140x=41x²+84x
2. действие: Заменяем x на -2
3. действие: 41(-2)²+84*(-2)=41(-2)²-84*2=-2(-41*2+84)=-2(-82+84)=-2*2=-4
ответ: -4