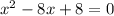
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
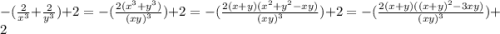
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
пусть производительности комбайнов равны х1 и х2. а их отношение t
запишем симтему трех уравнений t=x1/x2
x1+x2=1/12 (x1+x2)/x1*x2=50
подставляя выражение для х1 через t и x1/
x2(1+t)=1/12
(1+t)/x2*t=50
выражая х2 в первом уравнении получим квадратное уравнение относительно t
6t^2-13t+6=0 htшая которое получим t=1,5
ответ один комбайн работает в 1,5 раза быстрее второго