Дана функция f(x)= х² - 6х – 7 а) вычислите координаты вершины параболы;
б) запишите уравнение оси параболы;
в) найдите точки пересечения графика функции с осями координат;
г) постройте график заданной функции;
д) определите, в каких четвертях располагается график данной функции.
. 
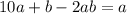
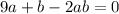
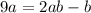
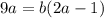
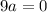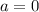- не підходить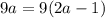
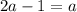
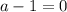
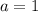
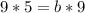
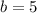
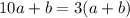
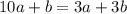
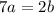
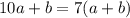
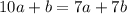
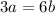
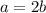
прямая проходит через точку M(10 ;2) значит должно выполняться условия
2 =k*10 +b;
y -2 =k*(x -10) *** уравнение прямой проходящей через точку M(10 ;2) *** ;
*** остается определить угловой коэффициент k .
для этого используем второе условие : она ┴ прямой с уравнением
48x+8y + 9 = 0 ⇒ y = -6x - 9/8 ⇒ k₁ = -6 ;
прямые перпендикулярны , если , k*k₁ = -1 ⇒k= -1/k₁ = -1/(-6) = 1/6.
y -2 =1/6*(x -10) ;
x -6y +2 =0 ;
определим точку A(x₁ ;0) пересечения этой прямой с осью x
x₁ - 6*0 +2 = 0 ⇒ x₁ = -2 .
Длина отрезка AO (расстояние этой точки до начала координат) = |-2|= 2.
(прямая линия не может отсекать отрезок от другой прямой: они могут пересекаться , совпадать или быть параллельными) .
ответ : 2 .