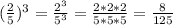
В решении.
Объяснение:
Решить квадратные уравнения:
1) х²-х-6= 0
D=b²-4ac =1+24=25 √D= 5
х₁=(-b-√D)/2a
х₁=(1-5)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(1+5)/2
х₂=3.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
2) х²+3х=4
х²+3х-4 =0
D=b²-4ac =9+16=25 √D= 5
х₁=(-b-√D)/2a
х₁=(-3-5)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-3+5)/2
х₂=2/2
х₂=1.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
3) х²=2х+8
х²-2х-8 =0
D=b²-4ac =4+32=36 √D= 6
х₁=(-b-√D)/2a
х₁=(2-6)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(2+6)/2
х₂=8/2
х₂=4.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
4) 25х²-1=0 (неполное квадратное уравнение).
25х² = 1
х² = 1/25
х = ±√1/25
х₁ = -1/5;
х₂= 1/5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
ответ: S5 = 1705
Объяснение:
Сначала найдем второй член геометрической прогрессии (b2). Его можно вычислить по формуле, когда известны предыдущий (b1) и следующий (b3) члены. bn = √bn-1 ⋅ bn+1; bn = √b1*b3 Подставляем наши значения: b2= √5*80=√400=20 Теперь мы знаем первые три последовательные члены геометрической прогрессии, значит можем найти ее знаменатель. Формула нахождения знаменателя q = bn+1 / bn Подставляем наши значения: q = b2 / b1 ; q =20/5=4 Осталось вычислить сумму первых пяти членов, для этого тоже есть специальная формула: Sn = b1 ⋅ (1 — qn) / (1 — q) S5 = 5 * (1-4^5) / (1-4) = 5* (1-1024)/ -3 = 5*(-1023)/-3 = -5115/-3 = 1705