1. Прилад, що складається з n блоків виходить з ладу, якщо відмовляє один блок. Блоки працюють незалежно один від одного. Надійність кожного блоку p.
Обчислити надійність приладу.
2. В урні 4 червоних, 5 синіх, 6 зелених куль. Навмання беруть 3 кулі. Яка
ймовірність того, що вони будуть однакового кольору або мати різні кольори.
3. Система має два незалежно працюючих елемента. Імовірність їх відмови
дорівнює 0,05 та 0,08 відповідно. Знайти ймовірність відмови системи, якщо для
цього достатньо відмови хоча б одного з елементів.
4. У майстерні на верстатах А, В, С виробляють 25%, 35% та 40% усіх деталей,
причому вони мають 15%, 12% та 6% браку відповідно. Знайти ймовірність того, що
навмання взята деталь – бракована.
5. У першій урні 2 білих та 4 чорних кулі, а у другій урні – 3 білих та 1 чорна
кулі. Із першої урни переклали у другу одну кулю. Знайти ймовірність того, що куля,
вийнята із другої урни після перекладання, буде білою.
6. У першому ящику 12 червоних та 6 білих куль. У другому – 15 червоних та
10 білих куль. Підкидають гральний кубик. Якщо випаде кількість очок кратна 3, то
навмання беруть кулю з першого ящика. Якщо випаде будь-яка інша кількість очок,
то беруть кулю з другого ящика. Яка ймовірність узяти червону кулю?
7. Серед N екзаменаційних білетів є n “щасливих”. Студенти підходять за
білетом один за одним. У кого більша ймовірність витягнути “щасливий” білет – у
того, хто тягне першим, чи у того, хто тягне білет другим?
8. У трьох ящиках маємо однакові деталі з різних заводів: у першому – 20
стандартних та 5 нестандартних деталей; у другому – 15 стандартних та 3
нестандартних; у третьому – 14 стандартних та 2 нестандартних. Із навмання взятого
ящика навмання взята деталь, яка виявилася стандартною. Знайти ймовірність того,
що цю деталь взято з першого ящика.
9. У першій урні 10 куль, з них 8 білих. У другій урні 20 куль, з них 4 білих. Із
кожної урни навмання взято по одній кулі, а потім із двох обраних навмання взято
одну. Знайти імовірність того, що остання куля буде білою.
10. У першому ящику 8 білих та 6 чорних куль. У другому – 10 білих і 4
чорних. Навмання вибирають ящик і кулю. Відомо, що витягнута куля чорна. Знайти
ймовірність того, що було обрано другий ящик.
 и
и 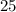 – среднеарифметическое равно
– среднеарифметическое равно 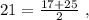 и при этом
и при этом  на
на 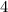 меньше двадцати пяти и на
меньше двадцати пяти и на 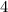 больше семнадцати.
больше семнадцати.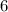 монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на 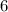 монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на 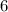 монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на 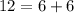 монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.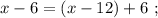
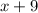 монет, а у Пети-II будет
монет, а у Пети-II будет 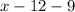 монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в 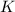 раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 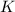 раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение: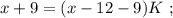


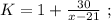
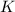 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 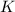 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда  откуда:
откуда: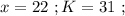
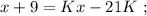
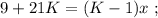
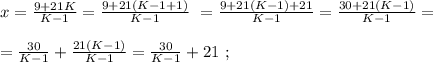

 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет  откуда:
откуда: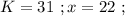
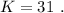
х-6=y+6
х-12=y
Значит, у них сейчас разница в 12 монет (у Васи на 12 монет больше, чем у Пети). Если же ещё и Петя даст 9 монет, то эта разница увеличится на 9+9 = 18 монет. Итого она будет составлять 12+18 = 30 монет.
Получается, что у Васи может в таком случае быть больше на 30 монет.
Если у одного минимальное количество монет (1 монета), то коэффициент K будет наибольший. А если у одного из них 1 монета, а у второго на 30 монет больше, то получается, что у второго — 31 монета. 31/1 = в 31 раз.
ответ: k = 31 (ответ Г)