 часа.
часа.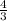 часа - 3 кг сплава
часа - 3 кг сплава кг сплава
кг сплава часа.
часа. часа - 3 кг сплава
часа - 3 кг сплава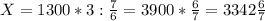 кг сплава
кг сплава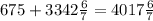 кг сплава
кг сплава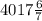 кг сплава.
кг сплава.
Решим дискриминант и после этого сделаем метод интервала.
x²-3x-4 < 0
Дискриминант:
x²-3x-4 = 0
D = b²-4ac => (-3)²-4*1*(-4) = 9+16 = 25 > 0, 2 корня.
√25 = 5 (можно и в уме)
x =
x₁ =
x₂ =
Корни уравнения: (x+1)(x-4)
На графике будет выглядеть так:
-∞ + - + +∞
00>
-1 4 x
Воспользуемся методом интервала, чтобы понять, в какое направление пойдёт решение:
f (x) = (x+1)(x-4)
f (2) = (2+1)(2-4) = 3*(-2) = -6
ответ: (-∞;-1) ∪ (4;+∞).
sinx/3=t
2-2t^2+3t=0
2t^2-3t-2=0
t1=-1/2
sinx/3=-1/2
x/3=(-1)^(k+1)П/6+Пk
x=(-1)^(k+1)П/2+3Пk
2) 2-2cos^23x-5cos3x-4=0
cosx=t
2-2t^2-5t-4=0
2t^2+5t+2=0
t=-1/2
cos3x=-1/2
3x=(П+-П/3)+2Пk
x=(П/3+-П/9)+2Пk/3