В решении.
Объяснение:
Дана функция у = х² + 6x – 7:
а) найдите нули функции;
Приравнять уравнение к нулю и решить как квадратное уравнение:
х² + 6x – 7=0
D=b²-4ac =36+28=64 √D=8
х₁=(-b-√D)/2a
х₁=(-6-8)/2
х₁= -14/2
х₁= -7;
х₂=(-b+√D)/2a
х₂=(-6+8)/2
х₂=2/2
х₂=1;
Точки пересечения графиком оси Ох х= -7; х=1, они являются нулями функции, так как значение у в этих точках равно нулю.
Координаты точек (-7; 0); (1; 0).
б) постройте график функции;
Построить график. График парабола со смещённым центром, ветви направлены вверх. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -8 -7 -6 -5 -4 -3 -2 -1 0 1 2
у 9 0 -7 -12 -15 -16 -15 -12 -7 0 9
в) найдите у (х= – 4).
При х= -4 у= -15.
Если в задании найти у(х-4)², это график параболы у=х² с центром в начале координат, смещённый по оси Ох вправо на 4 единицы.
Таблица:
х -4 -2 0 2 4
у 16 4 0 4 16.
Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
Поэтому, во-первых, нужно найти
и 
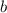- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от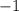
до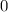 
(как результат приравнивания функций: 
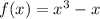), а второй - от 
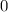до 
(здесь уже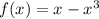 
):
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна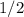
или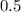 
(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
ответ: 0.5 .