
Делаем замену  .
.
Тогда 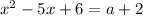
Получаем уравнение 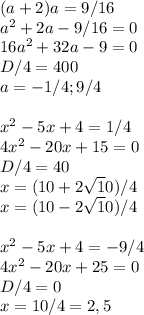
5; 9.
Объяснение:
Пусть 1 число Х, а второе - У.
Сумма их квадратов:
Х^2+У^2
Разность между суммой квад
ратов чисел Х и У и их удвоен
ной суммой:
Х^2+У^2-2ХУ
Составим первое уравнение
системы:
{Х^2+У^2-2ХУ=16
Среднее арифметическое чи
сел Х и У по определению:
(Х+У)/2
Составим второе уравнение сис
темы:
{(Х+У)/2=7
Осталось решить систему урав
нений:
{Х^2+У^2-2ХУ=16
{(Х+У)/2=7
Во втором уравнении Х выража
ем через У и подставляем в пер
вое:
{Х^2+У^2-2ХУ=16
{Х+У=14
{Х^2+У^2-2ХУ=16
{Х=14-У
(14-У)^2+У^2-2(14-У)У=16
196-28У+У^2+У^2-28У+2У^2-16=0
4У^2-56У+180=0 | :4
У^2-14У+45=0
D/4= 49-45=4=2^2>0
У_1=7-2=5
У_2=7+2=9
Х_1=14-У_1=14-5=9
Х_2=14-У_2=14-9=5
ответ: (9; 5)
(5; 9).
(x-1)(x-2)(x-3)(x-4)=9/16
(x-2)(x-3) = х² - 5х + 6
(х - 1)(х - 4) = х² - 5 х + 4 = (х² - 5х + 6) - 2
[(х² - 5х + 6) - 2]·(х² - 5х + 6) = 9/16
(х² - 5х + 6)² - 2·(х² - 5х + 6) - 9/16 = 0
замена у = х² - 5х + 6
у² - 2у - 9/16 = 0
D = 4 + 9/4 = 25/4
√D = 5/2
y₁ = (2 - 5/2):2 = -1/4
y₂ = (2 + 5/2):2 = 9/4
возвращаемся к замене
1) х² - 5х + 6 = -1/4
х² - 5х + 25/4 = 0
D = 25 - 25 = 0
x = 5/2 = 2,5
2) х² - 5х + 6 = 9/4
х² - 5х + 15/4 = 0
D = 25 - 15 = 10
√D = √10
x₁ = (5 - √10):2 = 2,5 - √2.5 = √2.5 (√2.5 - 1)
x₂ = (5 + √10):2 = 2,5 + √2.5 = √2.5 (√2.5 + 1)
ответ: уравнение имеет два различных корня
x₁ = √2.5 (√2.5 - 1) и x₂ = √2.5 (√2.5 + 1)
и кратный корень
х₃ = х₄ = 2,5