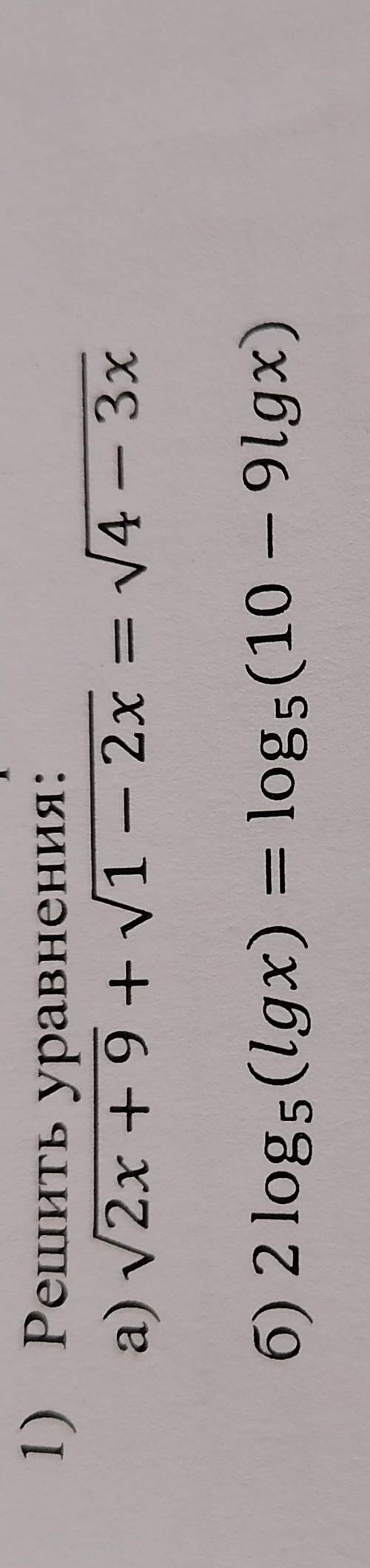
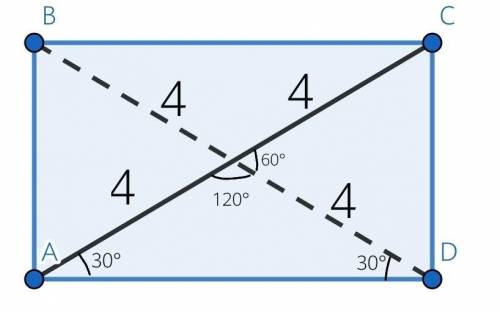
Проведем вторую диагональ, по теореме:
Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам.
В точке пересечения(обозначим буквой О) он делится на отрезки равным 4.
И получаем 4 равнобедренных треугольника у которых боковые стороны равны 4.
Рассмотрим треугольник АОD:
Поскольку треугольник равнобедренный то углы при основании равны(30°)
Зная что сумма внутренних углов треугольника составляет 180° найдём третий угол:
180-(30+30)=180-60=120°
Площадь треугольника:
S=1/2d²sin<a
S=1/2*8²*√3/2
S=16√3
ответ:площадь равна 16√3.
Дано уравнение cos a/2 + sin a/2 = -0,2 .
Пусть а/2 = х, применим формулу cos x = √(1 - sin²x).
Получаем √(1 - sin²x) + sin x = -0,2.
Перенесём sin х вправо и возведём обе части в квадрат.
1 - sin²x = (-0,2 - sin x)² = 0,04 + 0,4sin x + sin²x.
2sin²x + 0,4sin x - 0,96 = 0. Пусть sin x = t.
Ищем дискриминант:
D=0.4^2-4*2*(-0.96)=0.16-4*2*(-0.96)=0.16-8*(-0.96)=0.16-(-8*0.96)=0.16-(-7.68)=0.16+7.68=7.84;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(2root7.84-0.4)/(2*2)=(2.8-0.4)/(2*2)=2.4/(2*2)=2.4/4=0.6;
t_2=(-2root7.84-0.4)/(2*2)=(-2.8-0.4)/(2*2)=-3.2/(2*2)=-3.2/4=-0.8.
Отсюда видит, что есть 2 решения переменной (а/2) = х с учётом формул cos x = √(1 - sin²x) и условия cos (а/2) + sin (a/2)= -0,2.)
1) sin (a/2) = 0,6, cos (a/2) = -0,8,
2) sin (a/2) = -0,8, cos (a/2) = 0,6.
Для любого варианта синус двойного угла определится так:
sin a = 2sin(a/2)*cos(a/2) = 2*(-0,8)*0,6 = -0,96.
1
ОДЗ:
Проверка:
ответ: -4
2.
ОДЗ:
Второй корень не входит в ОДЗ
ответ: 10