1/(2х² + 5х) - 2/(25 - 10х) -4/(4х² - 25) = 1/5
1/[x(2x + 5)] - 2/[5(5 - 2x)] - 4/[(2x + 5)(2x - 5)] = 1/5
2x + 5 ≠ 0 ⇒ x ≠ -2,5
2x - 5 ≠ 0 ⇒ x ≠ 2,5
х ≠ 0
Cложим дроби: 1/[x(2x + 5)] - 4/[(2x + 5)(2x - 5) =
= (2х - 5 - 4х)/[x(2x + 5)(2x - 5)] =
= - (2x + 5)/[x(2x + 5)(2x - 5)] =
= 1/[x(5 - 2x)]
и ещё:
1/[x(5 - 2x)]- 2/[5(5 - 2x)] = (5 - 2x)/[5x(5 - 2x)] = 1/(5x)
вернёмся к уравнению
1/(5x) = 1/5
5x = 5
x = 1
А) x ≥ -6
Б) x ≥ 4,2
Объяснение:
А)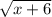 
Б) 
Эти выражения имеют смысл, пока подкоренное выражение не ушло в минус (ведь квадратный корень из отрицательного числа не извлекается, по крайней мере в действительных числах). Значит, нужно чтобы подкоренное выражение было больше или равно нулю.
x + 6 ≥ 0
далее просто решаем это неравенство- переносим числа в левую часть, меняя при этом их знак:
x ≥ -6 (вот и ответ на пункт А)
То есть, выражение 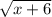имеет смысл при x ≥ -6
x - 4,2 ≥ 0
x ≥ 4,2 (ответ на пункт Б)
То есть, выражение имеет смысл при x ≥ 4,2
Прочтите статью еще раз и выберите правильный ответ. (A, B, C или D). В молодости Альберт Эйнштейн A не ходил в школу B плохо разбирался в математике C должен был сдавать экзамен дважды D был лучше по домашним предметам, чем другие В тексте B автор предполагает, что A ученый не проверял свои исследования B репортеры могли ошибиться C человеческий мозг не всегда активен D люди используют 90% своего мозга В тексте C автор говорит, что A в этой истории есть доля правдыB плохо разбирался в математике. C должен был сдать экзамен дважды. D был лучше по домашним предметам, чем другие. В тексте B автор предполагает, что A ученый не проверял свои исследования B репортеры могли ошибиться C человеческий мозг не всегда активны D люди используют 90% своего мозга В тексте C автор говорит, что A есть доля правды в рассказе B Ньютон часто лгал о своих теориях C История не очень известна D Ньютон никогда не видел падающих яблок
1/x(5+2x)-2/5(5-2x)-4/(2x-5)(5+2x)=1/5
5(2x-5)+2*x(2x+5)-4*5x=10x-25+4x^2+10x-20x=4x^2-25=(2x-5)(2x+5)
1/5x=1/5
x=1