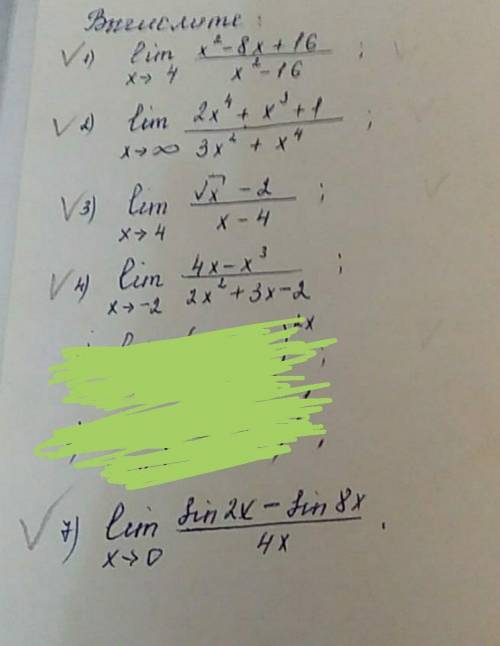
1. Сложим системы:
2x = 6
x = 3
Из первого уравнение y=2-x = 3-2 = -1
x=3 y=-1
2. Сложим системы
9x = 18
x = 2
Из второго 4y=8-3x=8-6=2 y=2/4=0,5
x=2 y=0,5 (2; 0,5)
3. Вычтем из первого уравнения второе
4x - 4x - 7y + 5y = 30 - 90
-2y = -60
y= 30
Из первого уравнения 4x = 30 + 7y = 30 + 210 = 240 x=60
x=60 y=30 (60;30)
4. Вычтем второе из первого
3y - 5y = 66 - 22
-2y = 44
y = -22
Из первого 12x = 66 - 3y = 66 + 66 = 132 x=11
x=11 y=-22 x+y=11-22= -11
5. Сложим уравнения
y-4y = 12
-3y = 12 y=-4
Из второго 2x=8+4y=8-16=-8 x=-4
x= -4 y=-4 x/y = 1
0,2,1/4,8/5,-3/2
Объяснение:
Заметим, что если подставим вместо переменной икс тоЮ к чему она стремится, везде(кроме второго) получим неопределенность 0/0. Такая неопределенность раскрывается либо правилом Лопиталя, но это обычно неприемлимый , либо выделением общих множителей. Итак,
1)x^2-8x+16=(x-4)^2
x^2-16=(x-4)(x+4) сократим на х-4, то х-4/х+4, подставим вместо х, то к чему он стремится, и получим 0/8, а это нуль
3)x-4=(√x-2)(√x+2), сокращаем на√x-2, получаем 1/4
4) сразу ничего очевидного нет, но мы не сдаемся, вынесем из числителя х, тогда х(4-x^2)=x(2-x)(2+x) а знаменатель разложим на множители, для этого приравняем его к нулю и найдем корни любым удобным , тогда получим корни -2 и 0.5, а значит изначальный знаменатель можно расписать как 2(x+2)(x-0,5) и вот уже видим на что можно сократить (х+2). Подставим вместо икс то, к чему он стремится, тогда -8/-5=8/5
7) sinα-sinβ=2sin(α-β)/2*cos(α+β)/2, вместо альфа 2х, вместо бетта 8х, следовательно, 2sin(-3x)*cos(5x), минус из синуса выносим как нечетность, тогда -2sin(3x)*cos(5x)/4x , теперь вычисляем как стандартный предел по частям, тогда получим 3/2 да еще минус от нечестности, -3/2
2) а теперь с бесконечность делить на бесконечность, нужно разделить на старшую степень числитель и знаменатель дроби, старшая степень 4, тогда
2+1/x+1/x^4 разделим на 3/x^2+1, теперь при подстановке вместо х бесконечности получим везде нули, кроме 2/1, а значит предел равен 2