Скорости изменения функций, это их производные
ОДЗ (3х-10)>=0 3x >= 10 x>=10/3
(14+6x)>=0 6x >= -14 x>=-14/6
f'(x) = 3/√(3x-10)
g'(x) = 6/√(14+6x)
3/√(3x-10) = 6/√(14+6x)
[3 √(14+6x)]² = [6 √(3x-10)]²
9(14+6x) = 36(3x-10)
126+54x = 108x-360
54x = 486
x = 9
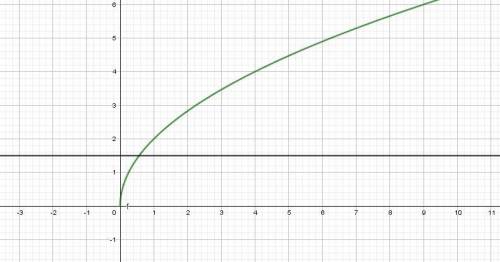
1) Построим графики функций 
и прямую параллельную оси ОХ 
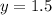
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
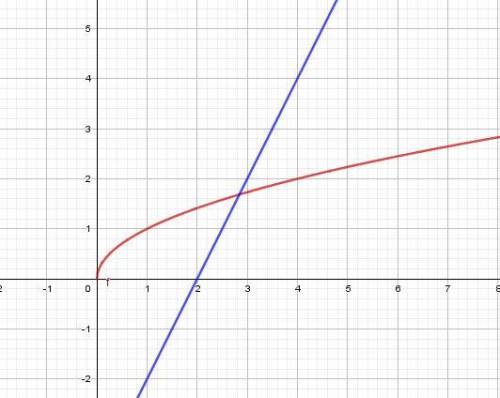
2) Построим график функции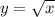 
и прямую 
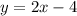проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков 
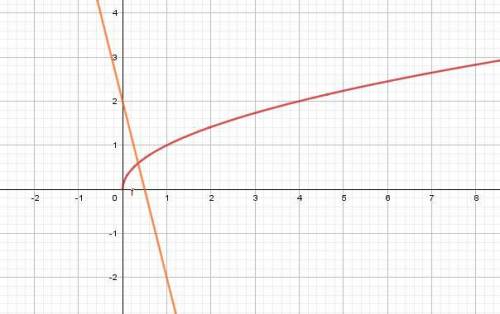
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна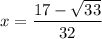 
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна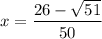 
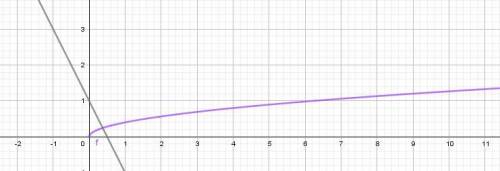
1) Построим графики функций и прямую параллельную оси ОХ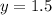
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
2) Построим график функции 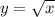и прямую 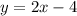проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна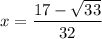
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна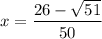
3/2sqrt(3x-10)=3/sqrt(14+6x)
sqrt(14+6x)=2sqrt(3x-10)
14+6x=4(3x-10)
14+6x=12x-40
54=6x
x=9