1)Для начала вспомним формулу дискриминанта:

2)Теперь разберемся с буквенными обозначениями в формуле а,b,c . Так a,b это коэффициенты ,стоящие перед переменными x, а с это последняя цифра без переменных,т.е:
ax^2+bx+с=0, где
a=1, так как перед икс в квадрате нету коэффициента, в этом случае он всегда равен 1;
b= 7, перед следующим икс стоит 7, это наш коэффициент b;
с=6, та самая цифра без переменных, типа икс.
3) Итак , разобрались , теперь Подставим в нашу формулу все наши данные:
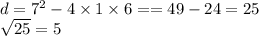
D>0, значит уравнение имеет 2 корня:

ответ:x1=1;x2=-6
корни=5 и 3