1)
1) Умножим обе части. = 3(х-1)-2(х+1)=6
2) Раскроем скобки. = 3х-3-2(х+1)=6 -> 3х-3-2х-2=6
3) Вычислим. = х-3-2=6 -> х-5=6
4) Переносим (-5) вправо. = х=6+5
5) Вычисляем и получаем: х = 11
ответ: х=11
2)
1) Раскроем скобки. = 2-х-2х+х(2)=(х+3)*(х-4) -> 2-х-2х+х(2)=х(2)-4х+3х-12
2) Уберём равные числа. = 2-х-2х=-4х+3х-12
3) Вычислим. = 2-3х=-4х+3х-12 -> 2-3х=-х-12
4) Переносим лишние числа (х) и (2) влево. = -3х+х=-12-2
5) Вычисляем. = -2х=-12-2 -> -2х=-14
6) Разделяем и получаем: х=7
ответ: х = 7
Разбор (2) после х, (2) означает степень.
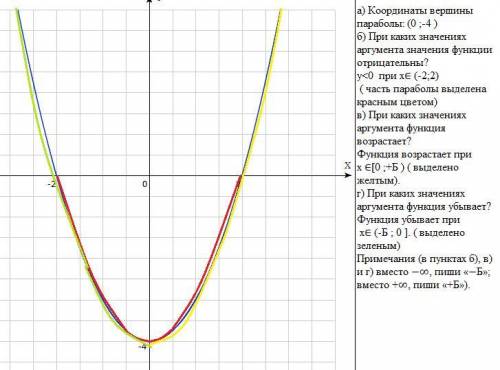
"Дана функция y=x2−4. Построй график функции y=x2−4.
a) Координаты вершины параболы: ( ; )
(в пунктах б), в) и г) вместо −∞, пиши «−Б»; вместо +∞, пиши «+Б»).
б) При каких значениях аргумента значения функции отрицательны?
( ; ). в) При каких значениях аргумента функция возрастает? [ ; ).
г) При каких значениях аргумента функция убывает? ( ; ]
(Сравни свой график с представленным в шагах решения).
Объяснение:
a) Координаты вершины параболы: х₀=0/2=0 , у₀=0-4=-4 ; (0 ;-4 ) .
б) у<0 при х²-4<0
-------(+)------(-2)--------(-)--------(2)------(+) ,при х∈ (-2;2)
в) Функция возрастает при х≥0.
г) Функция убывает при х≤0.