Алгебра: Знайдіть корінь рівняння 8x(в другому) -2=0

Знайдіть корінь рівняння 8x(в другому) -2=0

👇

Увидеть ответ

Ответ:

lerkina12

13.05.2020

x²-2=0

x²=2

x=±√2

ответ : √2 ; -√2.

4,6(35 оценок)

Открыть все ответы

Ответ:

432120

13.05.2020

Пусть х кг - первоначальная масса смеси, тогда

20 : х • 100% = $\frac{2000}{x}$ % - процентное содержание чечевицы в первоначальной смеси.

(х+25) кг - масса новой смеси, с добавлением 25кг чечевицы, тогда

(20+25) : (х+25) • 100% = 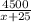$\frac{4500}{x+25}$ % - процентное содержание чечевицы в новой смеси.

По условию

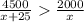$\frac{4500}{x+25}\frac{2000}{x}$ на 20%

Получаем уравнение:

$\frac{2000}{x}+20=\frac{4500}{x+25}$

ОДЗ: x>20

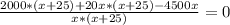
$\frac{2000*(x+25)+20x*(x+25)-4500x}{x*(x+25)}=0$

Дробь равна 0, если числитель равен 0, а знаменатель по ОДЗ не равен 0.

2000*(x+25)+20x*(x+25)-4500x=0

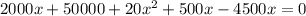
2000x+50000+20x^2+500x-4500x=0

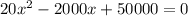
20x^2-2000x+50000=0

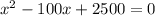
x^2-100x+2500=0

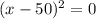
(x-50)^2=0

x=50

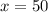
Проверка: х = 50 кг

20 : 50 • 100% = 40 % - процентное содержание чечевицы в первоначальной смеси.

45 : (50+25) • 100% = 60% - процентное содержание чечевицы в новой смеси.

60% - 40% = 20% удовлетворяет условию.

ответ: 50 кг

4,4(58 оценок)

Ответ:

Айка12341

13.05.2020

Поскольку функция содержит квадрат переменной х, то она квадратная. Следовательно, ее графиком будет парабола.

О параболе известно, что у нее есть вершина, что ветви ее могут быть направлены вверх или вниз, и что она может быть симметрична оси Оу.

Начнем с симметричности относительно оси Оу.

Если функция симметрична, то она называется четной. Свойство четности можно проверить, подставив вместо переменной х противоположное ей значение, то есть —х. Если в результате получим уравнение функции без изменений, то функция является четной, а значит симметричной относительно оси Оу.

Итак, проверим функцию на четность:

— функция четная.

Далее определим куда направлены ветви параболы. Для этого достаточно посмотреть на знак перед квадратом переменной х. в нашем случае перед ним стоит условно знак «плюс», а это значит, что ветви параболы будут направлены вверх.

Для определения координаты точки вершины параболы будем использовать готовую формулу, которая дает возможность найти значение первой координаты точки вершины параболы:

Чтобы получить значение второй координаты вершины подставим найденное значение х в уравнение функции:

Таким образом, вершиной параболы является точка (0; —4).

Теперь нужно вычислить еще какое-то количество точек, которые будут принадлежать параболе, для ее построения.

Возьмем четыре произвольных значения переменной х и посчитаем для них значение функции у:

х = 1: —точка (1; —3).

х = 2: —точка (2; 0).

х = —1: —точка (—1; —3).

х = —2: —точка (—2; 0).

Проведем через вершину и полученные точки кривую и получим график функции y = x^2 — 4.

4,8(90 оценок)

Это интересно:

Компьютеры-и-электроника