1) а1=-2 , d=3 , an=118-?
an=a1+(n-1)d
118= -2+(n-1)3
118= -2+3n-3
118 +5=3n
3n=123
n=41
a41=a1+40d= -2 + 120= 118 - является 41 членом арифметической прогрессии.
2) а39=83 ,d= -2 ,a1-?
a39=a1+ 38d
a1= a39 - 38d
a1= 83 - 38•(-2)=83 + 76=159
ответ: а1 = 159
3) а21= - 156, а34= -260, а1-? d-?
a21=a1 +20d --- a1=a21- 20d
a34=a1 +33d --- a1=a34- 33d
a1=a1
a21 -20d=a34 -33d
-20d+33d=a34-a21
13d= -260+156
13d=-104
d=-8
a1=a21-20d= -156-20•(-8)=-156+160= 4
ИЛИ:
а34=а1 + 33d
a34=a21+13d
a34-a21=13d
-260+156=13d
-104=13d
d=-8
a1=a34-33d=-260-33•(-8)=-260+264=4
5 (км/час) - скорость до встречи.
Объяснение:
Фродо с друзьями под предводительством Гэндальфа вышли из Шира. Путешествие в трактир «Гарцующий пони», в котором заночевали хоббиты и маг, проходило с разной средней скоростью — пока компания не наткнулась на назгула, дело шло быстрее, а после этой встречи бодрый дух друзей поугас, и они пошли медленнее на 4 км/ч. В целом расстояние до трактира составляло 12 км, которое было преодолено за 4 часа, причём первая и вторая части пути заняли одно и то же время. С какой скоростью происходило движение до встречи с назгулом?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость до встречи.
х-4 - скорость после встречи.
2 часа - время до встречи (по условию).
2 часа - время после встречи (по условию).
Расстояние общее известно, уравнение:
х * 2 + (х-4) * 2 = 12
2х+2х-8=12
4х=20
х=5 (км/час) - скорость до встречи.
5-4=1 (км/час) - скорость после встречи.
Проверка:
5*2 + 1*2 =10 + 2=12 (км), верно.
1. 2)
2. 3)
Объяснение:
1.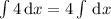 , интеграл
, интеграл 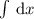 табличный и равняется
табличный и равняется 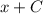 , тогда исходный равняется
, тогда исходный равняется 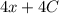 , произведение констант — тоже константа, поэтому решением будет
, произведение констант — тоже константа, поэтому решением будет 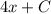 , что соответствует второму варианту ответа.
, что соответствует второму варианту ответа.
2. Область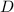 , ограниченная указанными кривыми
, ограниченная указанными кривыми 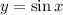 ,
, 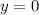 ,
,  и
и 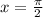 , показана на приложенном рисунке. Получается, что
, показана на приложенном рисунке. Получается, что 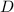 задают два неравенства,
задают два неравенства,  и
и 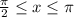 . Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
(Так получается, ибо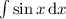 — табличный интеграл, равный
— табличный интеграл, равный 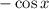 , а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть
, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть  , при известном
, при известном 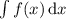 , то есть
, то есть 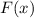 , притом константа в таком случае игнорируется.)
, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.