 функция
функция 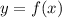 не существует. То есть найдем такие значения
не существует. То есть найдем такие значения  , при которых выражение
, при которых выражение 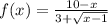 не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла: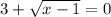 , однако понятно, что
, однако понятно, что 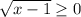 , значит знаменатель не обратиться в нуль.
, значит знаменатель не обратиться в нуль.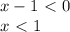
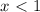 функции не существует. То есть она идет от
функции не существует. То есть она идет от  и куда-то дальше. Куда — нам пока неизвестно.
и куда-то дальше. Куда — нам пока неизвестно.  . Может быть она периодична?
. Может быть она периодична? 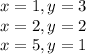
 , при котором числитель обратиться в нуль.
, при котором числитель обратиться в нуль. 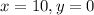
 повставлять разные значения (большие и маленькие).
повставлять разные значения (большие и маленькие). 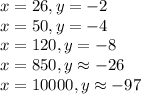
 уменьшается
уменьшается 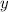 . Делаем вывод, что функция убывает бесконечно много. То есть
. Делаем вывод, что функция убывает бесконечно много. То есть 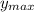 — не существует,
— не существует, 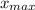 — не существует.
— не существует. 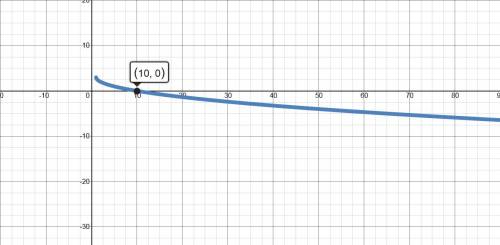
1) (0.25: 0)
Объяснение: