-2
Объяснение:
х^2+6х+9-2х+2-7=0
х^2+4х+4=0
Д= в^2-4ас= 4^2-4*1*4= 16-16=0
х= -4/2= -2
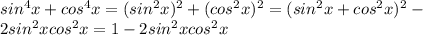
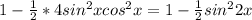
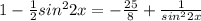
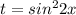 и продолжать решение уже дробно-рационального уравнения.
и продолжать решение уже дробно-рационального уравнения.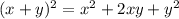
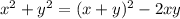
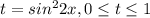
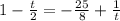
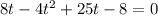
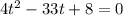
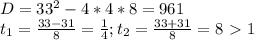 - этот корень не удовлетворяет нашему уравнению.
- этот корень не удовлетворяет нашему уравнению.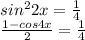
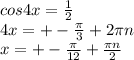
Обозначим длину одного катета а, второго - b.
Площадь прямоугольного треугольника находится по формуле:
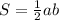 ,
,
где а, b - катеты.
В нашем случае:
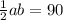
Отсюда аb=90:(1/2)
аb=90*2
ab=180
На каждом катете построили квадрат, затем нашли площади этих квадратов и полученные результаты сложили.
Чтобы найти площадь квадрата, нужно возвести длину его стороны во вторую степень. Площадь квадрата, построенного на катете а будет равна а². Площадь квадрата, построенного на катете b будет равна b². Складываем площади двух квадратов:
а²+b²=369
Из полученных двух уравнений с двумя неизвестными составляем систему:
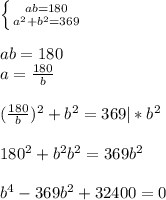

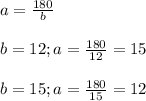
ответ: катеты прямоугольного треугольника равны 12 см и 15 см.
все рравильно и точно
Объяснение:
Это поавильно