Задача на уравнение касательной к графику функции. Решение см во вложении.
К сожалению файл не вставляется во вложение.
Начну писать так:
Задана функция f(x) = 3х^2-3x+c
В точке с координатой х = а касательная описывается уравнением y=3x+4. Угловой коэффициент этой прямой k = 3, это и есть значение производной функции в этой точке f'(a) = 3.
Найдём производную f'(x) = 6x - 3, тогда f'(а) = 6а - 3 = 3 и а = 1
найдём f(a) при а = 1 f(a)=3*1 - 3*1 +с = с
Уравнение касательной имеет вид: у = f(a) +f'(a)(x-a)
Подставим сюда y=3x+4, f(a) = с, f'(a) = 3 а=1
3x+4 = с +3*(х-1)
3x+4 =с +3х-3
4 = с -3
с=7
1.
а) 15·(-7) = -(15·7) = -105
б) -14·(-17) = 14·17 = 238
в) -0,9·4,1 = -(0,9·4,1) = -3,69
г)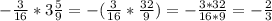
2.
а) -84:14 = -(84:14) = -6
б) -42:(-6) = 42:6 = 7
в) 0,114:(-0,76) = -(0,114:0,76) = -0,15
г)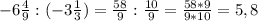
3.
а) -1,6b = -6,48
б) а:2,4 = -4,8
а = -4,8*2,4
а = -11,52
4.
Представьте числа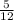
и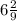 
в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
0,41(6)≈0,42
6,(2)≈6,222.
5.
|х|<86
-86<x<86
Целые неотрицательные решения неравенства: от 0 до 85. Общее количество 86.
Целые отрицательные решения неравенства: от -1 до -85. Общее количество 85.
Всего целых решений неравенства: 86+85 = 171.