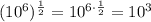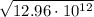. Чтобы извлечь его из под корня, нужно извлечь из под корня 
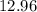, а затем 
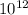. Если степень четная, то уменьшаем ее в 2 раза, если нечетная, то из под корня полностью число в этой степень извлечь нельзя.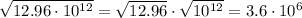 
![\sqrt[n]{a^m} = a^{\frac{m}{n}}](/tpl/images/0561/7515/fd5e1.png)
![a^{\frac{1}{2}} = \sqrt[2]{a^1} \\ a^{\frac{4}{2}} = \sqrt[2]{a^4} \\ a ^ {\frac{3}{6}} = \sqrt[6]{a^3} \\](/tpl/images/0561/7515/b4cce.png)
![\sqrt[2]{(10^6)^1}](/tpl/images/0561/7515/7734e.png)
. 
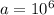возведено в 1 степень, то есть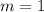
, степень корня — 2 (
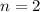). Перейдем от записи в виде корня к записи в виде степени:![\sqrt[2]{(10^6)^1} = (10^6)^{\frac{1}{2}}](/tpl/images/0561/7515/3f459.png)
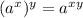, тогда:
