В математике существует 2 ограничения: 1) знаменатель дроби не должен равняться нулю; 2) подкоренное выражение может быть только больше или равно нулю.Второй вариант подходит в нашем случае)
ОТВЕТ: -2; -1; 0; 1; 2; 3; 4; 5.То есть, 8 целых решений.
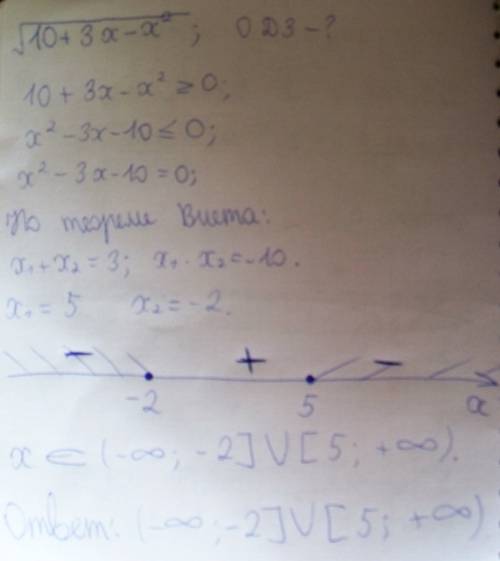
не уверен шо правельно но
обоих случаях у нас квадратная функция, значит, это графики парабол. Для их построения необходимо минимум 3 точки, одна из которых - это вершина параболы.
Вершина параболы имеет какие-то координаты (х;y).
Вершину можно найти по формуле х = - b/2a
Для случая а) а =1, b = -2, c = -8. Получаем координату х = 1. Подставляем щначение х в искомое выражение и получаем координаты вершины параболы (1; -9)
Для случая б) а = -1, b = 5, c = 0. Получаем координату х = 2.5. Подставляем щначение х в искомое выражение и получаем координаты вершины параболы (2.5; 5)
Теперь берём произвольное значение x и подставляем в функцию, таким образом получаем искомые графики.
На остальные вопросы легко ответить, смотря на график.
Подкоренное выражение должно быть болше или равно 0:
10+3x-x^2>=0
Разделим на -1
x^2-3x-10<=0
Решением этого неравенства будет промежуток:
-2<=x<=5
Количество целых решений на этом промежутке:
7 (-2, -1, 0,1, 2, 3, 4, 5)
ответ: 7