1)
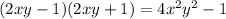
2)
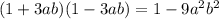
3)
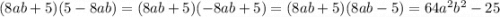
4)
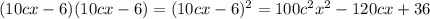
5)
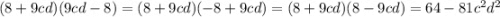
6)
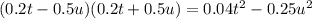
1. В первой части неравенства замечаем формулу сокращенного умножения "разность квадратов" , а вторую часть просто раскрываем по формуле квадрата суммы:
4x^2-25-(4x^2+12x+9)<или равен 2
Раскрываем скобки с противоположным знаком.
4x^2-25-4x^2-12x-9<или равен 2
Приводим подобные слагаемые. 4x^2 сокращаются.
-12x-34<или равен 2
-12x<или равен 36
Т.к. -12 с отрицательным знаком, меняем знак неравенства на противоположный., получим x>или равен 3.
2. Разложим множители по формуле разности кубов и получим: =(x-3y)(x^2+3xy+y^2)
3. Чтобы прямая и парабола пересекались, нужно, чтобы у них совпадали x и y. Тогда Составляем систему ур-ний из данных формул. Подставляем y=100 в ур-ние y=x^2.
100=x^2. отсюда x1=100, x2=-100. Получаем точки: (100;100) и (-100;100)
1) (2xy - 1)(2xy + 1) = (2xy)² - 1² = 4x²y² - 1
2) (1 + 3ab)(1 - 3ab) = 1 - (3ab)² = 1 - 9a²b²
3) (8ab + 5)(5 - 8ab) = (5 + 8ab)(5 - 8ab) = 5² - (8ab)² = 25 - 64a²b²
4) наверно в одной из скобок знак плюс :
(10cx - 6)(10cx + 6) = (10cx)² - 6² = 100c²x² - 36
Если в двух скобках минусы, то :
(10cx - 6)(10cx - 6) = (10cx - 6)² = 100c²x² - 120cx + 36
5) (0,2t - 0,5u)(0,2t + 0,5u) = (0,2t)² - (0,5u)² = 0,04t² - 0,25u²