
x є [1/2;1)
Объяснение:
x<1
4x>=2
x принадлежит от 1/2 включительно, до 1 не включаючи
Пусть х км/ч - скорость течения реки, тогда (30 - х) км/ч - скорость катера против течения, (30 + х) км/ч - скорость катера по течению. Уравнение:
84/(30-х) - 32/(30+х) = 2
84 · (30 + х) - 32 · (30 - х) = 2 · (30 + х) · (30 - х)
2520 + 84х - 960 + 32х = 2 · (30² - х²)
116х + 1560 = 1800 - 2х²
116х + 1560 - 1800 + 2х² = 0
2х² + 116х - 240 = 0
Сократим обе части уравнения на 2
х² + 58х - 120 = 0
D = b² - 4ac = 58² - 4 · 1 · (-120) = 3364 + 480 = 3844
√D = √3844 = 62
х₁ = (-58-62)/(2·1) = (-120)/2 = -60 (не подходит, так как < 0)
х₂ = (-58+62)/(2·1) = 4/2 = 2
ответ: 2 км/ч - скорость течения.
Главное избавиться от корней в разности корней, для этого функцию и умножают на выражение, сопряжённое разности корней.
Сопряжённое выражение - это то же выражение, но с противоположным знаком.
Умножим и числитель, и знаменатель на СУММУ тех же корней. В итоге в числителе получится разность квадратов, и корни в числителе сгорят.
Бояться этой суммы корней в знаменателе не стоит, просто продолжим упрощать выражение насколько возможно, а затем просто подставим число, к которому стремится предел. И получится ответ, идеально подходящий к имеющемуся у вас шаблону.
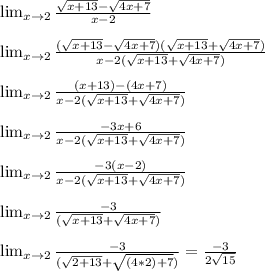
[0,5;1)