В коробке 6 кубиков с буквами A, A, R, K, E, T. Какова вероятность того, что слово РАКЕТА появится, когда вы потянете кубики один за другим? 2. По цели было выпущено 2 пули. Если у первого есть шанс 5/6 поразить цель за один выстрел, а у второго шанс поразить цель 6/7, найдите вероятность того, что оба не поразят цель.
3. Брошены 2 кубика. Найдите вероятность того, что сумма любых очков делится на 5.
4. Какова вероятность того, что пуля не поразит цель за один выстрел 2 / 5.3? Какова вероятность того, что пуля не поразит цель дважды за один выстрел?
5. Первый ящик содержит 6 белых и 4 черных шара, а второй ящик содержит 7 белых и 3 черных шара. Из каждой коробки вынимали один мяч за другим. Найдите вероятность того, что полученные шары разные.
6. Вероятность возникновения события A по крайней мере в одном из 4 экспериментов составляет 0,9984. Какова вероятность появления события А в одном эксперименте?
7. Вероятность того, что событие A произойдет по крайней мере в одном из 4 экспериментов, составляет 0,9744. Найдите вероятность того, что событие А не появится в одном эксперименте.
8. Монета подбрасывается 6 раз. Найдите вероятность того, что «герб» появится 5 раз.
9. 10 из 25 студентов в группе обучаются бесплатно. Найдите вероятность того, что все 7 случайно выбранных студентов будут учиться бесплатно.
 км/мин.
км/мин.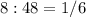 км/мин.
км/мин.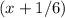 км/мин.
км/мин.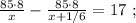
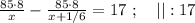
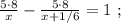
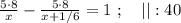
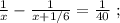
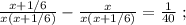
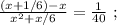
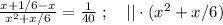
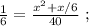
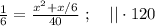
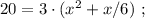
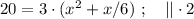
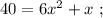
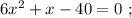
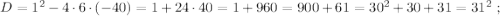
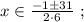
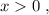 так, как это скорость,
так, как это скорость,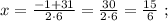
Выразим а2, а4 , а6 через первый член арифметической прогрессии и разность прогрессии (d)
a2=a1+d a4=a1+3d a6=a1+5d и подставим в систему:
{a1+a1+5d=11 a1+d+a1+3d=10
{2a1+5d=11 2a1+4d=10
Решим систему методом сложения. Умножим первое уравнение на (-1) и сложим со вторым:
{-2a1-5d=-11 + 2a1+4d=10
-d=-1
d=1
2a1+4=10
a1=3 (подставили найденное значение d во второе уравнение системы и нашли первый член прогрессии.)
По формуле суммы n-первых членов прогрессии найдём сумму первых шести членов этой прогрессии:
S6=(2·3+5 )\2·6=33 (Sn=(2a1+d(n-1))\2·n)
ответ:33