
24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
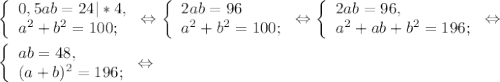

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
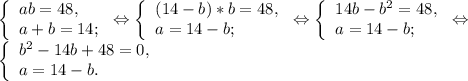
Решим квадратное уравнение:
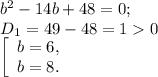
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
2 см и 2 см
Объяснение:
Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию
y'=(4·x–x²)'=4–2·x.
Находим критические точки функции:
y'=0 ⇔ 4–2·x=0 ⇔ x=2 – критическая точка.
Проверим знаки производной:
при x<2: y'=4–2·x>0 и при x>2: y'=4–2·x<0.
Значит, x=2 точка максимума. Тогда
yмакс=y(2)=4·2–2²=8–4=4 см²,
а стороны x=2 см и 4–2=2 см.