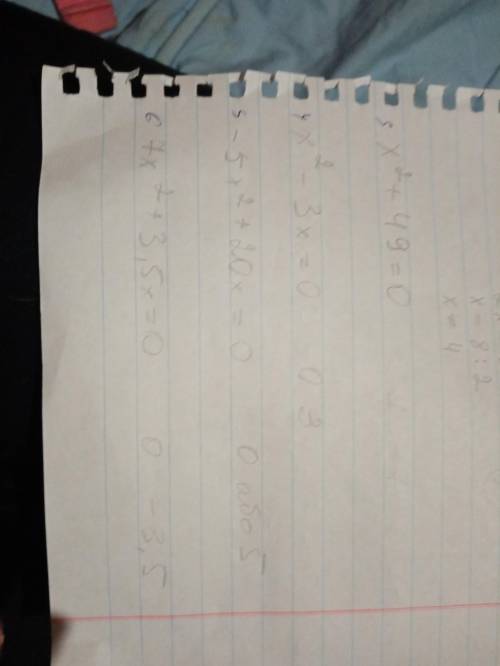
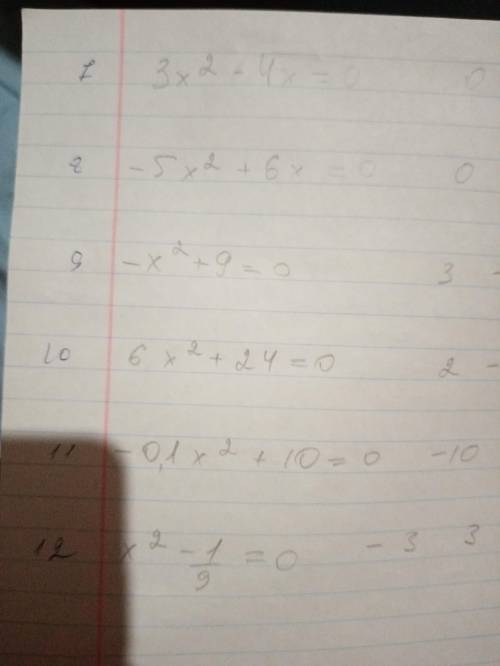
Объяснение:
a) -4x-6x<<1-3, -10x<<-2, x>>0,2 и 3x-2x<10-9, x<1,
[0,2](1) , отв. [0,2; 1)
b) 5x-4x<-3-8, x<-11 и 7x-8x>5+2, -x>7, x<-7, (-11)(-7)
ответ: (-~;-11)
2) умножим все на 4, -4<1+2x<12, -4-1<2x<12-1, -5<2x<11, делим на 2,
-2,5<x<5,5 ответ: (-2,5; 5,5)
3) систему решаем (x-1)/2>>0 и 3-1/4*x>>0, x-1>>0, x>>1 и
(12-х)/4 >>0 , 12-x>>0, -x>>-12, x<<12, ответ: [1;12]
Движение по течению: собственная скорость катера плюс скорость течения реки.
Движение против течения: собственная скорость катера минус скорость течения реки.
Находим разницу между скоростями по течению и против течения, и результат делим на 2, так как скорость течения реки учитывается в обоих случаях.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Расстояние между пристанями примем за единицу (целое).
1) 1 : 3 = 1/3 - скорость катера по течению реки;
2) 1 : 4 = 1/4 - скорость катера против течения реки;
3) 1/3 - 1/4 = 4/12 - 3/12 = 1/12 - разница;
4) 1/12 : 2 = 1/12 · 1/2 = 1/24 - скорость течения реки;
5) 1 : 1/24 = 1 · 24/1 = 24 (ч) - время движения плота.
ответ: за 24 часа.
1) 3х2 - 4х = 0
x(3x-4)=0 -- выносим общий множитель
3x-4=0
x = 4/3 (дробь) или х = 0 (имеет два решения)
8) -5х2 + 6х = 0
x (5x+6) = 0 -- выносим общий множитель
x = 0
5x +6 = 0
x = - 5/6 (дробь) или х = 0 (имеет два решения)
9) -х2 + 9 = 0
- х2 = - 9
х2 = 9
х = 3 или х = -3 (имеет два решения)
10) 6х2 + 24 = 0
х2 = -4
Утверждение ложно для любого значения х, поскольку парная степень всегда положительна или 0.
Поэтому, здесь можно написать "Решений нету"
11) -0,1х2 + 10 = 0
х2 + 100 = 0
х2 = -100
Утверждение ложно для любого значения х, поскольку парная степень всегда положительна или 0.
Поэтому, здесь можно написать "Решений нету"
12) х2 - 1/9 = 0
9х2 - 1 = 0
9х2 = 1
х2 = 1/9
х = 1/3 или -1/3 (дробь) (имеет два решения)
3) х2 + 49 = 0
х2 = -49
Утверждение ложно для любого значения х, поскольку парная степень всегда положительна или 0.
Поэтому, здесь можно написать "Решений нету"
4) х2 - 3х = 0
х (х-3) = 0 -- выносим общий множитель
х - 3 = 0
х = 0 или х = 3 (имеет два решения)
5) -5х2 + 20х = 0
-5х * (х-4) = 0 -- выносим общий множитель
х * (х-4) = 0
х - 4 = 0
х = 0 или х = 4 (имеет два решения)
6) 7х2 + 3.5х = 0
2х2 + х = 0
х(2х+1)=0 -- выносим общий множитель
х = 0
2х+1 = 0
х = 0 или х = -1/2(дробь) (имеет два решения)
Вроде-бы все решила, что было на фото )