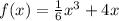
Задание 1:
Общий вид линейной функции: у = kx + b.
Число k является угловым коэффициентом. Если он отрицательный (меньше нуля), то функция убывает, а если положительный (больше нуля), то функция возрастает.
Взглянем на данную функцию:
y = 3x + 2
k = 3 > 0, поэтому функция возрастает.
Задание 2:
y = 2x + 3 — это линейная функция. Она достигает наибольшего и наименьшего значений на концах отрезка.
Вычислим их, подставив числа на концах промежутка [-1;3] в формулу:
у (-1) = 2 * (-1) + 3 = 1;
у (3) = 2 * 3 + 3 = 9.
Теперь выберем из полученных значений наименьшее и наибольшее.
Таким образом:
у наим. = 1;
у наиб. = 9.
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».