Два фермера, работая вместе, могут вспахать поле за 25 часов.
Производительность труда у первого и второго относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?
Пусть Х-производительность 1-го, У-производительность 2-го.
Система:
х+у=125
2х=5у
Последовательно:
2х+2у=2/25
2х-5у=0
7у=2/25 и у=2175
Тогда х=135
Итак, производительности мы нашли.
Поочередно фермеры работали 45,5 часа = 91/2 часа.
Пусть из этого времени 2-ой работал Т часов, тогда 1-ый работал 912-Т часов.
Уравнение:
(91/2-Т)⋅(1/35)+Т⋅(2/175)=1
имеет корень Т=17,5
Проверка.
1. проверим , что х+у=125
1/35+2/175=(70+175)/(175⋅35)=7/175=1/25
2. проверим, что 2х=3у:
2/35=5⋅2/175
3. Проверим уравнение при поочередной работе:
Если 2-ой работал 17,5 часов, то 1-ый работал 45,5-17,5=28 часов
28⋅135+(352)⋅(2175)=28/35+1/5=1
ОТВЕТ: 17,5
Пусть за 
час 1-й кран будет наполнять весь бассейн
за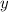 
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
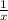- объем воды, который проходит через 1-й кран за 1 час.
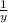- объем воды, который проходит через 2-й кран за 1 час.
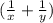- общая производительность двух кранов.
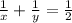- первое уравнение
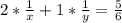- второе уравнение
Из первого уравнения получим: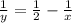 
и вставим во второе уравнение:
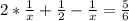
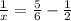
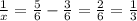
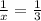
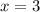
Подставим 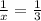в первое уравнение:
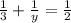
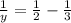
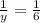
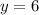
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
Пусть в первом x а во втором y. Тогда
x+y=75
и
4*1,5x/5=y+2
Из первого выразим x=75-y
Подставим в уже упрощенную уравнение:
6x=5y+10
получим
6(75-y)=5y+10
450-6y=5y+10
11y=440
y=40, значит x=35