Для доказательство просто рассмотрим два случая: когда 
- нечетное и когда - четное.
1). - нечетное, то есть 
.
При всех нечетных натуральных число 
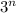имеет остаток 
при делении на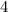 
.
число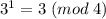 
. При 
получаем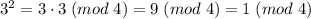 
. Дальше, при 
: 
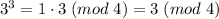. Как видим, круг замкнулся и на нечетных будет выскакивать остаток при делении 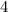, а при четных - 
.Также, при любом натуральном значении число 
имеет остаток при делении на .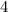
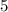, возводимое в степень, равняется по модулю 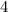.Третье слагаемое: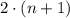 
будет нацело делиться на :
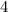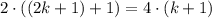
Значит, если - нечетное, то:
При нечетных все, как видите, сходится.
2). - четное, или же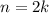 
.
Как мы определили ранее, в этом случае 
и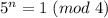 
.
При этом второе слагаемое:
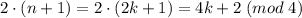
Найдем всю сумму:
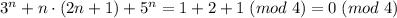
И при четных утверждение работает.
Как известно, каждое натуральное число либо четное, либо нечетное (третьего не дано) и никаких других натуральных чисел, которые не являются четными и не являются нечетными одновременно, науке неизвестно.
Так что мы рассмотрели все случаи, и в каждом из них результат был равен 
, то есть делился на .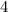
решение на фотографиях