Волшебный праздничек Рождества моя семейство празднует любой год. Обыкновение намереваться всей семьей за большущим столом присутствовала сколько я себя помню. Дед всякий раз посиживает на знатном и ведает ситуации из собственной жизни. Почти все его рассказы мы знаем на память, но любой один заботливо Ему хорошо наше забота. Наряженная елка мигает разноцветными светом и пахнет мандаринами и жареной уткой. Целый денек перед праздничным днем заполнен сутолокой и ожиданием чуда. Новогодний сочельник для меня полон чудес. Всякий раз что-нибудь случается, чего не ожидаешь. Прибывают постояльцы, коим всякий раз прежде. У матери внезапно выходит самый благовидный и аппетитный тортик. Или же я нахожу под подушкой кусок мяса, бережно спрятанный котом.
Ну мне кажется,Набоков был очень смелым,у него была только одна цель - преодоление страха смерти. Исконная экзистенциальная неувязка боязни погибели и отчаяния перед её лицом делается предметом изучения.Набоков избирает самую трагическую историю - основатель, теряющий отпрыска. Это несчастье ненормально и вследствие того неутешно. Погибель отпрыска – воплощение исконного людского боязни, победа над жизнью. В заключении помереть самому функционирует иная ипостась погибели – смерть-избавительница. Например собственно что в том числе и испуг погибели не одергивает героя.
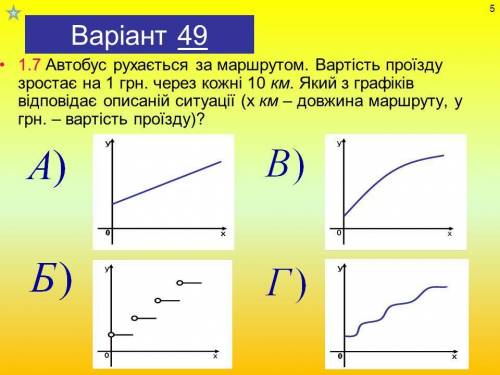
7/Задание № 4:
Назовите такое значение параметра a, при котором неравенство ax>7x+2 не имеет решений.
ax>7x+2
ax-7x>2
(a-7)x>2
Если а=7, то неравенство 0>2 не имеет решений.
Если а>7, то решения x>2/(a-7)
Если а<7, то решения x<2/(a-7)
ОТВЕТ: 7
7/Задание № 3:
Сколько корней имеет уравнение: |x+2+|−x−4||−8=x?
|x+2+|−x−4||−8=x
|x+2+|x+4||−8=x
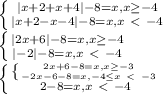
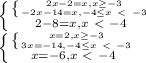
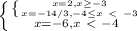
Условию раскрытия моделей соответствуют только первый и третий корни 2 и -6.
ОТВЕТ: 2 корня
7/Задание № 1:
Сколько чётных двузначных чисел, которые при делении на сумму цифр числа дают неполное частное 7 и остаток 3?
РЕШЕНИЕ: Пусть это число АВ=10a+b. Тогда, 10a+b=7(a+b)+3.
10a+b=7a+7b+3
3a=6b+3
a=2b+1
2b=a-1
Учитывая, что:
- а и b цифры, то есть целые числа от 0 до 9, но а не ноль, поскольку AB двузначное число
- число AB должно быть четным, то проверять нечетные b нет смысла
- остаток должен быть меньше делителя, значит минимально возможная сумма (a+b) равна 4
b=0: a=2*0+1=1 - не может быть a+b=1<4
b=2: a=2*2+1=5, число 52
b=4: a=2*4+1=9, число 94
При b=6 и более а=2*6+1=13 и более - не соответствует цифре.
ОТВЕТ: 2 числа
правильний график пид буквою б