План действий такой: 1) ищем производную 2) приравниваем её к нулю и решаем уравнение 3) полученные корни ставим на числовой прямой и определяем знак производной на каждом участке 4) делаем выводы: а) где плюс, там возрастание, где минус - убывание, точка, при переходе через которую производная меняет знак с + на -, это точка максимума, наоборот - точка минимума. начали? 1) производная равна(-2х(х +2) - ( 3 - х²)·1)/(х + 2)² 2) ( -2х² - 4х - 3 + х² )/(х + 2)² = 0 | ·(х + 2 ) ≈ 0 -2х² - 4х -3 +х² = 0 -х² -4х -3 = 0 х² + 4х + 3 = 0 х1 = -1; х2 = -3 3) -∞ + -3 - -1 + +∞ 4) функция возрастает при х∈( -∞; -3)∨(-1; +∞) функция убывает при х ∈(-3; -1) х = -3 точка мак4симума х = -1 точка минимума.
Произведение равно 0, если один из множителей равен 0. (x+1,5)=0 ИЛИ корень из (х^2-4x-5)=0
ОПРЕДЕЛЯЕШЬ ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ. ОДЗ первого уравнения: Х принадлежит от (-оо до +оо) ОДЗ второго уравнеиня: х принадлежит от (-оо до -1 включая -1 U от 5 включая 5 до +оо)
РЕШАЕШЬ КАЖДОЕ ПОЛУЧИВШИЕСЯ УРАВНЕНИЕ ОТДЕЛЬНО.(x+1,5)=0 х=-1,5 *и второе тоже решаешь. Должен получиться ответ: Корнем первого уравнения является: -1,5 Корнями второго уравнения являются: -1 и 5
Далее чертишь числовую прямую, отмечаешь на ней ОДЗ двух уравнений. По рисунку смотришь, какое значение коря удовлетворяет и первому ОДЗ и второму.
8 и 8
Объяснение:
Пусть 1е число х, тогда 2е - 16-х. Значение их произведения задается функцией f(x)=x(16-x)
f(x)= -x²+16x
Функция квадратичная с а<0 (т.е. ветви вниз), значит ее наибольшее значение находится в вершине.
Х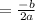
Х = -16:(-2) = 8.
Тогда 2е число 16-8=8.
P.S. вот морока. Но так запомни: произведение тем больше, чем меньше разница между числами при фиксированной их сумме.