S = 4
Объяснение:
Найдём уравнение прямой, проходящей через точки (-3; 0) и (-1; 3).
(х + 3)/(-1 + 3) = (у -0)/(3 - 0)
3(х + 3) = 2у
у = 1,5х + 4,5
Найдём точки пересечения этой прямой с осью Ох
у = 0;
1,5х + 4,5 = 0
х = -3
парабола у = 3х касается оси Ох в точке х = 0.
Найдём точки пересечения параболы у = 3х² и прямой у = 1,5х + 4,5
3х² = 1,5х + 4,5
3х² - 1,5х - 4,5 = 0
2х² - х - 3 = 0
D = 1 + 24 = 25
x1 = (1 - 5)/4 = -1
x2 = (1 + 5)/4 = 1.5
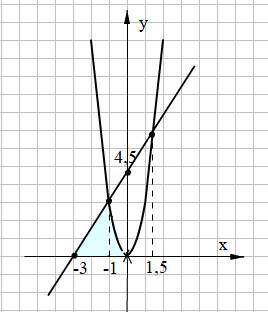
Изобразим графики, заданные уравнениями параболы и прямой.
Смотри рисунок на прикреплённом файле.
Очевидно, что фигура, заключённая между параболой, наклонной прямой и осью Ох, представляет собой криволинейный треугольник. Причем левая половина этого треугольника ограничена наклонной прямой и осью Ох, а правая половина - параболой и осью Ох. Соответственно, и интегралов будет два
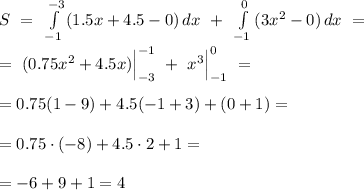
{ b₃ =8 ; b₅ =2⇔{ b₁q² =8 ; b₁q⁴ =2.⇔ {b₁q² =8 ;q² =2/8 .⇔
{ b₁*1/4 =8 ;q² =1/4. {b₁ =32 ; [ q = -1/2 ; q =1/2. ⇔( совокупности систем)
[ { b₁ =32 ; q = -1/2 ; { b₁ =32 ; q =1/2 .
---
a) { b₁ =32 ; q = -1/2.
S₆ =b₁(1-q⁶)/(1-q) = 32(1-(-1/2)⁶) /(1-(-1/2)) =32(1-1/64) /(1+1/2) =21.
---
b) { b₁ =32 ; q =1/2.
S₆ =b₁(1-q⁶)/(1-q) = 32(1-(1/2)⁶) /(1-1/2)) =32(1-1/64) /(1-1/2) =63.
ответ : {21 ; 63}.
* * * * * * *
32 ; -16 ; 8 ; -4 ; 2 ; -1 ; ...
32 ; 16 ; 8 ; 4 ; 2 ;1 ;...