Объяснение:
24.121
я, конечно прощения, но члены арифметической прогрессии обозначаются как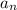 
(у вас это 
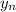) а разность арифметической прогрессии обозначается как b (у вас это d) я буду обзначать так, как принято в математике
1)
а₁₀ = -19
d= -2
применим формулу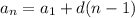 
a₁₀ = a₁ + (-2)*9 = -19 a₁ = -19 +18 = -1
2)
применим ту же формулу
a₅ = a₁ +4d = 13 ⇒ a₁ = 13-4d
a₁₆ = a₁ + 15d = 46 подставим сюда a₁ = 13-4d получим
13-4d +15d = 46 ⇒ 11d = 33 ⇒ d = 3
тогда
a₁ = 13-4d = 13 - 12 = 1
24.123
всё та же формула
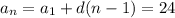
8 +3(n-1) = 24
8+3n -3 = 24
3n = 24-5 = 17 здесь нет целого решения для n ⇒ 24 не есть член арифметической прогрессии
2. Анализ равенства показывает, что в его левой части имеется сумма двух слагаемых, каждый из которых представляет собой значение тангенс функции для различных углов. Первое слагаемое, после применения переместительного свойства сложения к его аргументу, примет вид tg(2 * π + 2 * х), а формула приведения tg(2 * π + α) = tgα позволит его записать как tg(2 * x).
3. Для преобразования второго слагаемого вспомним о периодичности тангенс функции. Как известно, тангенс функция имеет наименьший положительный период, равный π. Следовательно, из аргумента выражения tg(7 * π – 2 * x) можно отбросить 7 * π. Тогда, tg(7 * π – 2 * x) = tg(-2 * x). Наконец, учитывая нечётность тангенс функции, левая часть доказываемого равенства примет вид: tg(2 * x) + tg(–2 * x) = tg(2 * x) - tg(2 * x) = 0. Что и требовалось доказать.