Алгебра: Сделайте уравнение замени.

Сделайте уравнение замени.

👇

Увидеть ответ

Ответ:

deulinslava26

15.10.2020

ОДЗ: (То чему x НЕ равен чтобы уравнение имело смысл)

a не равен 0

x^2 - 3x не равен 0

x не равен 0 и x не равен 3

(3x^2-9x)/2-12/(x^2-3x)=3

3·(x^2-3x)/2-12/(x^2-3x) = 3

Пусть a=x^2-3x

3a/2-12/a=3 умножим обе части уравнения на a

3a^2/2-3a-12=0

D=9+4*12*3/2=9^2

a1=2(3+9)/6=4

a2=2(3-9)/6=-2

Теперь сделаем обратную замену. У нас получится два уравнения

x^2-3x=4

x^2-3x-4=0

D=9+4*4=5^2

x1=(3+5)/2=4

x2=(3-5)/2=-1

x^2-3x=-2

x^2-3x+2=0

D=9-4*2=1

x1=(3+1)/2=2

x2=(3-1)/2=1

x1=4

x2=-1

x3=2

x4=1

4,8(33 оценок)

Открыть все ответы

Ответ:

Angelina123321123321

15.10.2020

Точка x0 называется точкой максимума функции f(x), если существует такая окрестность точки x0, что для всех x ≠ x0 из этой окрестности выполняется неравенство f(x)< f(x0).Точка x0 называется точкой минимума функции f(x), если существует такая окрестность точки x0, что для всех x ≠ x0 из этой окрестности выполняется неравенство f(x)> f(x0).Точки минимума и точки максимума называются точками экстремума.Теорема. Если x0 – точка экстремума дифференцируемой функции f(x), то f ′(x0) =0.Точки, в которых функция имеет производную, равную нулю, или недифференцируема (не имеет производной), называют критическими точками. Точки, в которых производная равна 0, называют стационарными.Геометрический смысл: касательная к графику функции y=f(x) в экстремальной точке параллельна оси абсцисс (OX), и поэтому ее угловой коэффициент равен 0 ( k = tg α = 0).Теорема: Пусть функция f(x) дифференцируема на интервале (a;b), x0 С (a;b), и f ′(x0) =0. Тогда:1) Если при переходе через стационарную точку x0 функции f(x) ее производная меняет знак с «плюса» на «минус», то x0 – точка максимума.2) Если при переходе через стационарную точку x0 функции f(x) ее производная меняет знак с «минуса» на «плюс» , то x0 – точка минимума. ПРАВИЛО нахождения наибольшего и наименьшего значения функции f(x) на отрезке [a;b]. 1. Найти призводную функции и приравнять нулю. Найти критические точки.2. Найти значения функции на концах отрезка, т.е. числа f(a) и f(b).3. Найти значения функции в тех критических точках, которые принадлежат [a;b].4. Из найденных значений выбрать наибольшее и наименьшее. ПРАВИЛО нахождения минимума и максимума функции f(x) на интервале (a;b).1. Найти критические точки f(x) (в которых f ′(x)=0 или f(x) не существует) .2. Нанести их на числовую прямую (только те, которые принадлежат (a,b) ).f ′(x) + – +
a x0x1 bf (x) / \ /3. Расставить знаки производной в строке f ′(x) , расставить стрелки в строке f(x).4. x max = x0, x min = x1.5. y max = y(x0), y min = y(x1).

4,6(47 оценок)

Ответ:

marianachornii

15.10.2020

Объяснение:

y = |x-4| + |x+1|

Итак, имеем функцию с двумя модулями. Под модулями стоят выражения вида g(x)=x-a

На промежутке (a; +∞), g(x) > 0

На промежутке (-∞; a), g(x) < 0

При x=a, g(x) = 0

Этот анализ понять, что наш график будет иметь три состояния, когда оба модуля раскрываются со знаком +, когда оба модуля раскрываются со знаком -, и когда они раскроются с разными знаками

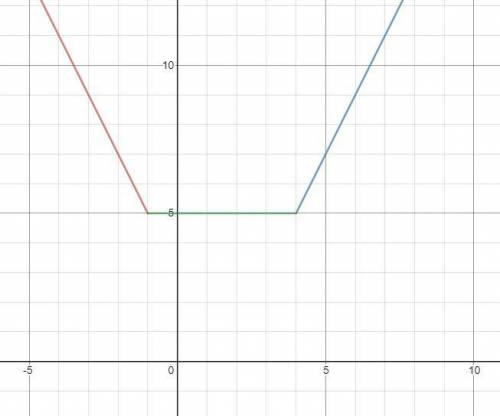
Рассмотрим случай, когда -1 > x. Оба подмодульных выражения примут отрицательные значения. Модули раскроются со знаком минус. y = -(x-4) - (x+1) = -2x + 3Рассмотрим случай, когда -1 <= x < 4. Тогда первый модуль откроется со знаком -, а второй со знаком плюс. y = -(x-4) + x + 1 = 5Рассмотрим случай, когда 4 <= x. Тогда оба модуля откроются со знаком плюс. y = x - 4 + x + 1 = 2x - 3

Имеем 3 промежутка, на каждом из которых своя прямая. Такой график иногда называют "корыто". Две боковые прямые образуют "стенки", а "дно" образовано горизонтальной линией.

Осталось построить вышеперечисленные 3 функции, но учитывая их промежуток. График приложен.