От имени Министерства спорта Российской Федерации и себя лично приветствую участников, организаторов и гостей Международного турнира по профессиональному боевому самбо «ПЛОТФОРМА S-70»!
Наш отечественный вид борьбы – самбо – давно признан во всём мире и продолжает активное развитие. Возникшая на его базе прикладная дисциплина – боевое самбо – является одним из наиболее захватывающих и зрелищных видов современных спортивных единоборств.
За последние четыре года турниры серии «LEAGUE S-70» стали одними из самых знаковых спортивных событий в нашей стране, к ним приковано внимание СМИ и многих поклонников единоборств. Отмечу, что турнир стал объединяющим фактором спортсменов России и ближнего зарубежья, так как, участвуя в нём, славную школу самбо проходят всё новые и новые поколения единоборцев из Украины, Казахстана, Болгарии и других зарубежных государств.
Уверен, турнир откроет новые имена талантливых спортсменов, подарит любителям самбо множество эмоций и незабываемые впечатления от яркого спортивного зрелища.
Желаю участникам Международного турнира «ПЛОТФОРМА S-70» удачи, успехов, захватывающих поединков и заслуженных побед!
[ ]
]
Объяснение:
(m - 3)x² - 6x + m + 5 = 0
Имеет корни, если Д≥0.
Д=36-4*(m - 3)*(m + 5 )=-4m²-8m +96=-4(m²+2m-12).
-4<0 ⇒ (m²+2m-12)≤0 .
Корни m²+2m-12=0 ,Д=4+48=52=4*13
х1=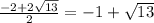
х2=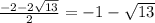
m²+2m-12≤0 , метод интервалов
+ + + + [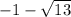 ]- - - - - - - {
]- - - - - - - {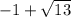 ]+ + + + + +
]+ + + + + +
х∈{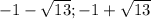 ]
]
Исследуем знаки корней при различных m.
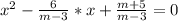
Если 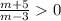 , то корни одинаковых знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни одинаковых знаков если m∈(-∞ ;-5)∪(3 ;+∞).
, то корни одинаковых знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни одинаковых знаков если m∈(-∞ ;-5)∪(3 ;+∞).
Если 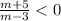 , то корни разных знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни разных знаков знаков если m∈(-5 ; 3 ).
, то корни разных знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни разных знаков знаков если m∈(-5 ; 3 ).
Если 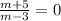 ,т.е m=-5 то уравнение x²+
,т.е m=-5 то уравнение x²+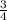 *x=0 и корни 0 и -3\4.
*x=0 и корни 0 и -3\4.
значит
ответ: при
2)
Графиком функции является парабола, ветви направлены вверх, (0;0) - координаты вершины параболы.
Опустим график функции на 4 единицы вниз, то вершина параболы переместится в точку и получаем график функции
Область значений функции: . Наименьшее значение у=-4, а наибольшего нет.
ответ: наименьшее значение функции равен -4, а наибольшего нет.