ОЧЕНЬ запишіть проміжки зростання і спадання функції y=-x квадраті +3x-5

👇

Увидеть ответ

Открыть все ответы

Ответ:

Perestroika

11.06.2020

1)Найдите девятый член последовательности

$\displaystyle y_n=\frac{n^2+2}{n-7}$

$\displaystyle y_9=\frac{9^2+2}{9-7}=\frac{81+2}{2}=41.5$

2) Найдите пятый член последовательности заданной рекуррентным у1 = ½, yₙ=2*y₍ₙ₋₁₎

y₂=2*1/2=1; y₃=2*1=2; y₄=2*2=4; y₅=2*4=8

3) Подберите формулу n- го члена последовательности - 2/2; 4/5; - 6/8; 8/11; -10/14;

$\displaystyle a_n=\frac{(-1)^n*(2*n)}{2+3(n-1)}$

проверка:

$\displaystyle n=1: a_1=\frac{(-1)^1*2*1}{2+3(1-1)}=-\frac{2}{2}\\\\n=2: a_2=\frac{(-1)^2*2*2}{2+3(2-1)}=\frac{4}{5}\\\\n=3:a_3=\frac{(-1)^3*2*3}{2+3(3-1)}=\frac{-6}{8}$

4) Сколько членов последовательности 3, 6, 9, 12,….меньше числа 95

аₙ=а₁+3(n-1)

aₙ<95

a₁+3(n-1)<95

3+3n-3<95

3n<95

n<31.(6)

n=31

проверим: a₃₁=3+3(31-1)=3+3*30=93

Значит 31 член меньше 95

5) у₁ = 2, у₂ = 1, уₙ = 2y₍ₙ₋₂₎+3y₍ₙ₋₁₎ (n = 3,4,5,…).Найдите n, если известно, что уₙ = 83.

тут можно просто решить находя слены этой последовательности

y₁=2

y₂=1

y₃=2*2+3*1=4+3=7

y₄=2*1+3*7=2+21=23

y₅=2*7+3*23=14+69=83

N=5

4,7(32 оценок)

Ответ:

maria22890

11.06.2020

x=1.

Объяснение:

если комбинировать методы, можно решить таким путём:

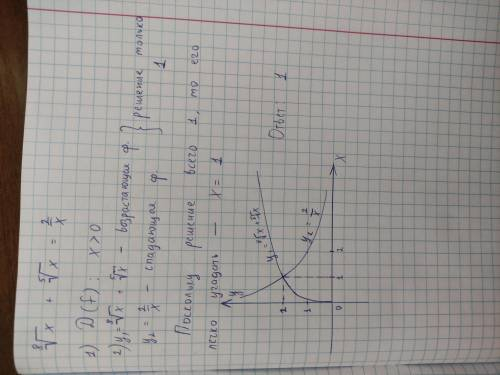
1) ОДЗ уравнения базируется на дроби (х≠0) и на корне чётной степени (х≥0), то есть только положительные значения Х являются допустимыми в данном уравнении;

2) левая часть исходного уравнения представляет из себя одну ветви параболы, которая лежит в первой координатной четверти; правая же часть - гиперболу, ветви которой лежат в первой и третьей четвертях. Как вывод: при таких графиках только одна точка пересечения, то есть только один корень;

3) если в исходном уравнении сделать замены вида

$x=t^{40}; \sqrt[8]{x}=t^5; \sqrt[5]{x}=t^8,$

тогда исходное уравнение (ОДЗ: только положительные числа) становится таким:

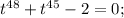
$t^{48}+t^{45}-2=0;$

где элементарным подбором видно (теорема Безу), что t=1;

4) если понижать степень в уравнении пункта №3, тогда получается, что

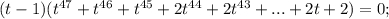
$(t-1)(t^{47}+t^{46}+t^{45}+2t^{44}+2t^{43}+...+2t+2)=0;$

дальнейшее понижение степени полинома 47-й степени не есть целесообразно, так как согласно пункту №2 уравнение имеет единственный действительный корень. Это х=1.